Mar 22, 2025 9 min read ลองฟอร์มของไดโน

สรุป Mastering Bitcoin: Programming the Open Blockchain บทที่ 4

Keys and Addresses

อลิซต้องการจ่ายเงินให้กับบ๊อบแต่โหนดของบิตคอยน์ในระบบหลายพันโหนดจะตรวจสอบธุรกรรมของเธอ โดยไม่รู้ว่าอลิซหรือบ๊อบเป็นใคร ละเราต้องการรักษาความเป็นส่วนตัวของพวกเขาไว้เช่นนี้ อลิซจำเป็นต้องสื่อสารว่าบ๊อบควรได้รับบิตคอยน์บางส่วนของเธอโดยไม่เชื่อมโยงแง่มุมใด ๆ ของธุรกรรมนั้นกับตัวตนในโลกจริงของบ๊อบ หรือกับการชำระเงินด้วยบิตคอยน์ครั้งอื่น ๆ ที่บ๊อบได้รับ อลิซใช้ต้องทำให้มั่นใจว่ามีเพียแค่บ๊อบเท่านั้นที่สามารถใช้จ่ายบิตคอยน์ที่เขาได้รับต่อไปได้

ในบิตคอยน์ไวท์เปเปอร์ได้อธิบายถึงแผนการที่เรียบง่ายมากสำหรับการบรรลุเป้าหมายเหล่านั้น ดังที่แสดงในรูปด้านล่างนี้

ตัวของผู้รับอย่างบ๊อบเองจะได้รับบิตคอยน์ไปยัง public key ของเขาที่ถูกลงนามโดยผู้จ่ายอย่างอลิซ โดยบิตคอยน์ที่อลิซนำมาจ่ายนั้นก็ได้รับมาจากที่ใครสักคนส่งมาที่ public key ของเธอ และเธอก็ใช้ private key ของเธอในการลงนามเพื่อสร้างลายเซ็นของเธอและโหนดต่าง ๆ ของบิตคอยน์จะทำการตรวจสอบว่าลายเซ็นของอลิซผูกมัดกับเอาต์พุตของฟังก์ชันแฮชซึ่งตัวมันเองผูกมัดกับ public key ของบ๊อบและรายละเอียดธุรกรรมอื่นๆ

ในบทนี้เราจะพิจารณาpublic key private key Digital signatrue และ hash function จากนั้นใช้ทั้งหมดนี้ร่วมกันเพื่ออธิบาย address ที่ใช้โดยซอฟต์แวร์บิตคอยน์สมัยใหม่

Public Key Cryptography (การเข้ารหัสของ public key)

ระบบเข้ารหัสของ public key ถูกคิดค้นขึ้นในทศวรรษ 1970 มาจากรากฐานทางคณิตศาสตร์สำหรับความปลอดภัยของคอมพิวเตอร์และข้อมูลสมัยใหม่

นับตั้งแต่การคิดค้นระบบเข้ารหัส public key ได้มีการค้นพบฟังก์ชันทางคณิตศาสตร์ที่เหมาะสมหลายอย่าง เช่น การยกกำลังของจำนวนเฉพาะและการคูณของเส้นโค้งวงรี โดยฟังก์ชันทางคณิตศาสตร์เหล่านี้สามารถคำนวณได้ง่ายในทิศทางหนึ่ง แต่เป็นไปไม่ได้ที่จะคำนวณในทิศทางตรงกันข้ามโดยใช้คอมพิวเตอร์และอัลกอริทึมที่มีอยู่ในปัจจุบัน จากฟังก์ชันทางคณิตศาสตร์เหล่านี้ การเข้ารหัสลับช่วยให้สามารถสร้างลายเซ็นดิจิทัลที่ไม่สามารถปลอมแปลงได้และบิตคอยน์ได้ใช้การบวกและการคูณของเส้นโค้งวงรีเป็นพื้นฐานสำหรับการเข้ารหัสลับของมัน

ในบิตคอยน์ เราสามารถใช้ระบบเข้ารหัส public key เพื่อสร้างคู่กุญแจที่ควบคุมการเข้าถึงบิตคอยน์ คู่กุญแจประกอบด้วย private key และ public key ที่ได้มาจาก private key public keyใช้สำหรับรับเงิน และ private key ใช้สำหรับลงนามในธุรกรรมเพื่อใช้จ่ายเงิน

ความสัมพันธ์ทางคณิตศาสตร์ระหว่าง public key และ private key ที่ช่วยให้ private key สามารถใช้สร้างลายเซ็นบนข้อความได้ ลายเซ็นเหล่านี้สามารถตรวจสอบความถูกต้องกับ public key ได้โดยไม่เปิดเผย private key

TIP: ในการใช้งานซอฟแวร์กระเป๋าเงินบิตคอยน์บสงอัน จะทำการเก็บ private key และ public key ถูกเก็บไว้ด้วยกันในรูปแบบคู่กุญแจเพื่อความสะดวก แต่อย่างไรก็ตาม public key สามารถคำนวณได้จาก private key ดังนั้นการเก็บเพียง private key เท่านั้นก็เป็นไปได้เช่นกัน

bitcoin wallet มักจะทำการรวบรวมคู่กุญแต่ละคู่ ซึ่งจะประกอบไปด้วย private key และ public key โดย private key จะเป็นตัวเลขที่ถูกสุ่มเลือกขึ้นมา และเราขะใช้เส้นโค้งวงรี ซึ่งเป็นฟังก์ชันการเข้ารหัสทางเดียว เพื่อสร้าง public key ขึ้นมา

ทำไมจึงใช้การเข้ารหัสแบบอสมมาตร

ทำไมการเข้ารหัสแบบอสมมาตรจึงถูกใช้บิตคอยน์? มันไม่ได้ถูกใช้เพื่อ "เข้ารหัส" (ทำให้เป็นความลับ) ธุรกรรม แต่คุณสมบัติที่มีประโยชน์ของการเข้ารหัสแบบอสมมาตรคือความสามารถในการสร้าง ลายเซ็นดิจิทัล private key สามารถนำไปใช้กับธุรกรรมเพื่อสร้างลายเซ็นเชิงตัวเลข ลายเซ็นนี้สามารถสร้างได้เฉพาะโดยผู้ที่มีความเกี่ยวข้องกับ private key เท่านั้น แต่อย่างไรก็ตาม ทุกคนที่สามารถเข้าถึง public key และธุรกรรมสามารถใช้สิ่งเหล่านี้เพื่อ ตรวจสอบ ลายเซ็นได้ คุณสมบัติที่มีประโยชน์นี้ของการเข้ารหัสแบบอสมมาตรทำให้ทุกคนสามารถตรวจสอบลายเซ็นทุกรายการในทุกธุรกรรมได้ ในขณะที่มั่นใจว่าเฉพาะเจ้าของ private key เท่านั้นที่สามารถสร้างลายเซ็นที่ถูกต้องได้

Private keys

private key เป็นเพียงตัวเลขที่ถูกสุ่มขึ้น และการควบคุม private key ก็เป็นรากฐานสำคัญที่ทำให้เจ้าชองกุญแจดอกนี้สามารถควบคุมบิตคอยน์ทั้งหมดที่มีความเกี่ยวข้องกับ public key ที่คู่กัน private key นั้นใช้ในการสร้างลายเซ็นดิจิทัลที่ใช้ในการเคลื่อนย้ายบิตคอยน์ เราจำเป็นต้องเก็บ private key ให้เป็นความลับตลอดเวลา เพราะการเปิดเผยมันให้กับบุคคลอื่นนั้นก็เปรียบเสมือนกับการนำอำนาจในการควบคุมบิตคอยน์ไปให้แก่เขา นอกจากนี้ private key ยังจำเป็นต้องได้รับการสำรองข้อมูลและป้องกันจากการสูญหายโดยไม่ตั้งใจ เพราะหากเราได้ทำมันสูญหายไป จะไม่สามารถกู้คืนได้ และบิตคอยน์เหล่านั้นจะถูกปกป้องโดยกุญแจที่หายไปนั้นตลอดกาลเช่นกัน

TIP: private key ของบิตคอยน์นั้นเป็นเพียงแค่ตัวเลข คุณสามารถสร้างมันได้โดยใช้เพียงเหรียญ ดินสอ และกระดาษ โดยการโยนเหรียญเพียง 256 ครั้งจะทำให้คุณได้เลขฐานสองที่สามารถใช้เป็น private key ของบิตคอยน์ จากนั้นคุณสามารถใช้มันในการคำนวณหา public key แต่อย่างไรก็ตาม โปรดระมัดระวังเกี่ยวกับการเลือใช้วิธีการสุ่มที่ไม่สมบูรณ์ เพราะนั่นอาจลดความปลอดภัยของ private key และบิตคอยน์ที่มัมปกป้องอยู่อย่างมีนัยสำคัญ

ขั้นตอนแรกและสำคัญที่สุดในการสร้างกุญแจคือการหาแหล่งที่มาของความสุ่มที่ปลอดภัย (ซึ่งเรียกว่า เอนโทรปี) การสร้างกุญแจของบิตคอยน์นั้นเกือบเหมือนกับ "เลือกตัวเลขระหว่าง 1 และ 2^256" ซึ่งวิธีที่แน่นอนที่คุณใช้ในการเลือกตัวเลขนั้นไม่สำคัญตราบใดที่มันไม่สามารถคาดเดาหรือทำซ้ำได้ โดยปกติแล้วซอฟต์แวร์ของบิตคอยน์มักจะใช้ตัวสร้างตัวเลขสุ่มที่มีความปลอดภัยทางการเข้ารหัสเพื่อสร้างเอนโทรปี 256 บิต

สิ่งที่สำคัญในเรื่องนี้คือ private key สามารถเป็นตัวเลขใดๆ ระหว่าง 0 และ n - 1 (รวมทั้งสองค่า) โดยที่ n เป็นค่าคงที่ (n = 1.1578 × 10^77 ซึ่งน้อยกว่า 2^256 เล็กน้อย) ซึ่งกำหนดอยู่ใน elliptic curve ที่ใช้ใน Bitcoin ในการสร้างกุญแจดังกล่าว เราสุ่มเลือกเลขขนาด 256 บิตและตรวจสอบว่ามันน้อยกว่า n ในแง่ของการเขียนโปรแกรม โดยปกติแล้วสิ่งนี้ทำได้โดยการป้อนสตริงของบิตสุ่มที่ใหญ่กว่า ซึ่งรวบรวมจากแหล่งที่มาของความสุ่มที่มีความปลอดภัยทางการเข้ารหัส เข้าไปในอัลกอริทึมแฮช SHA256 ซึ่งจะสร้างค่าขนาด 256 บิตที่สามารถตีความเป็นตัวเลขได้อย่างสะดวก หากผลลัพธ์น้อยกว่า n เราจะได้กุญแจส่วนตัวที่เหมาะสม มิฉะนั้น เราก็เพียงแค่ลองอีกครั้งด้วยตัวเลขสุ่มอื่น

คำเตือน: อย่าเขียนโค้ดของคุณเองเพื่อสร้างตัวเลขสุ่ม หรือใช้ตัวสร้างตัวเลขสุ่ม "แบบง่าย" ที่มีให้ในภาษาโปรแกรมของคุณ ใช้ตัวสร้างตัวเลขสุ่มเทียมที่มีความปลอดภัยทางการเข้ารหัส (CSPRNG) จากแหล่งที่มีเอนโทรปีเพียงพอ ศึกษาเอกสารของไลบรารีตัวสร้างตัวเลขสุ่มที่คุณเลือกเพื่อให้มั่นใจว่ามีความปลอดภัยทางการเข้ารหัส การใช้งาน CSPRNG ที่ถูกต้องมีความสำคัญอย่างยิ่งต่อความปลอดภัยของกุญแจ

ต่อไปนี้คือกุญแจส่วนตัว (k) ที่สร้างขึ้นแบบสุ่มซึ่งแสดงในรูปแบบเลขฐานสิบหก (256 บิตแสดงเป็น 64 หลักเลขฐานสิบหก โดยแต่ละหลักคือ 4 บิต):

1E99423A4ED27608A15A2616A2B0E9E52CED330AC530EDCC32C8FFC6A526AEDD

TIP: จำนวนที่เป็นไปได้ของ private key ทั้งหมดนั้นมีอยู่ 2^256 เป็นตัวเลขที่ใหญ่มากจนยากจะจินตนาการได้ มันมีค่าประมาณ 10^77 (เลข 1 ตามด้วยเลข 0 อีก 77 ตัว) ในระบบเลขฐานสิบ เพื่อให้เข้าใจง่ายขึ้น ลองเปรียบเทียบกับจักรวาลที่เรามองเห็นได้ซึ่งนักวิทยาศาสตร์ประมาณการว่ามีอะตอมทั้งหมดประมาณ 10^80 อะตอม นั่นหมายความว่าช่วงค่าของกุญแจส่วนตัว Bitcoin มีขนาดใกล้เคียงกับจำนวนอะตอมทั้งหมดในจักรวาลที่เรามองเห็นได้

การอธิบายเกี่ยวกับวิทยาการเข้ารหัสแบบเส้นโค้งวงรี (Elliptic Curve Cryptography)

วิทยาการเข้ารหัสแบบเส้นโค้งวงรี (ECC) เป็นประเภทหนึ่งของการเข้ารหัสแบบอสมมาตรหรือ public key ซึ่งอาศัยหลักการของปัญหาลอการิทึมแบบไม่ต่อเนื่อง โดยแสดงออกผ่านการบวกและการคูณบนจุดต่างๆ ของเส้นโค้งวงรี

บิตคอยน์ใช้เส้นโค้งวงรีเฉพาะและชุดค่าคงที่ทางคณิตศาสตร์ ตามที่กำหนดไว้ในมาตรฐานที่เรียกว่า secp256k1 ซึ่งกำหนดโดยสถาบันมาตรฐานและเทคโนโลยีแห่งชาติ (NIST) เส้นโค้ง secp256k1 ถูกกำหนดโดยฟังก์ชันต่อไปนี้ ซึ่งสร้างเส้นโค้งวงรี: y² = (x³ + 7) บนฟิลด์จำกัด (F_p) หรือ y² mod p = (x³ + 7) mod p

โดยที่ mod p (มอดูโลจำนวนเฉพาะ p) แสดงว่าเส้นโค้งนี้อยู่บนฟิลด์จำกัดของอันดับจำนวนเฉพาะ p ซึ่งเขียนได้เป็น F_p โดย p = 2^256 – 2^32 – 2^9 – 2^8 – 2^7 – 2^6 – 2^4 – 1 ซึ่งเป็นจำนวนเฉพาะที่มีค่ามหาศาล

บิตคอยน์ใช้เส้นโค้งวงรีที่ถูกนิยามบนฟิลด์จำกัดของอันดับจำนวนเฉพาะแทนที่จะอยู่บนจำนวนจริง ทำให้มันมีลักษณะเหมือนรูปแบบของจุดที่กระจัดกระจายในสองมิติ ซึ่งทำให้ยากต่อการจินตนาการภาพ อย่างไรก็ตาม คณิตศาสตร์ที่ใช้นั้นเหมือนกับเส้นโค้งวงรีบนจำนวนจริง

ตัวอย่างเช่น การเข้ารหัสลับด้วยเส้นโค้งวงรี: การแสดงภาพเส้นโค้งวงรีบน F(p) โดยที่ p=17 แสดงเส้นโค้งวงรีเดียวกันบนฟิลด์จำกัดของอันดับจำนวนเฉพาะ 17 ที่มีขนาดเล็กกว่ามาก ซึ่งแสดงรูปแบบของจุดบนตาราง

เส้นโค้งวงรี secp256k1 ที่ใช้ในบิตคอยน์สามารถนึกถึงได้ว่าเป็นรูปแบบของจุดที่ซับซ้อนมากกว่าบนตารางที่มีขนาดใหญ่มหาศาลจนยากจะเข้าใจได้

ตัวอย่างเช่น จุด P ที่มีพิกัด (x, y) ต่อไปนี้เป็นจุดที่อยู่บนเส้นโค้ง secp256k1:

P =
        (55066263022277343669578718895168534326250603453777594175500187360389116729240,
        32670510020758816978083085130507043184471273380659243275938904335757337482424)

เราสามารถใช้ Python เพื่อยืนยันว่าจุดนี้อยู่บนเส้นโค้งวงรีได้ตามตัวอย่างนี้:
ตัวอย่างที่ 1: การใช้ Python เพื่อยืนยันว่าจุดนี้อยู่บนเส้นโค้งวงรี

Python 3.10.6 (main, Nov 14 2022, 16:10:14) [GCC 11.3.0] on linux
        Type "help", "copyright", "credits" or "license" for more information.
        > p = 115792089237316195423570985008687907853269984665640564039457584007908834671663
        > x = 55066263022277343669578718895168534326250603453777594175500187360389116729240
        > y = 32670510020758816978083085130507043184471273380659243275938904335757337482424
        > (x ** 3 + 7 - y**2) % p
        0

ผลลัพธ์เป็น 0 ซึ่งแสดงว่าจุดนี้อยู่บนเส้นโค้งวงรีจริง เพราะเมื่อแทนค่า x และ y ลงในสมการ y² = (x³ + 7) mod p แล้ว ทั้งสองด้านของสมการมีค่าเท่ากัน

ในคณิตศาสตร์ของเส้นโค้งวงรี มีจุดที่เรียกว่า "จุดที่อนันต์" (point at infinity) ซึ่งมีบทบาทคล้ายกับศูนย์ในการบวก บนคอมพิวเตอร์ บางครั้งจุดนี้แทนด้วย x = y = 0 (ซึ่งไม่เป็นไปตามสมการเส้นโค้งวงรี แต่เป็นกรณีพิเศษที่สามารถตรวจสอบได้ง่าย)

มีตัวดำเนินการ + ที่เรียกว่า "การบวก" ซึ่งมีคุณสมบัติคล้ายกับการบวกแบบดั้งเดิมของจำนวนจริงที่เด็กๆ เรียนในโรงเรียน เมื่อมีจุดสองจุด P1 และ P2 บนเส้นโค้งวงรี จะมีจุดที่สาม P3 = P1 + P2 ซึ่งอยู่บนเส้นโค้งวงรีเช่นกัน

ในเชิงเรขาคณิต จุดที่สาม P3 นี้คำนวณได้โดยการลากเส้นระหว่าง P1 และ P2 เส้นนี้จะตัดกับเส้นโค้งวงรีที่จุดเพิ่มเติมอีกหนึ่งจุดพอดี เรียกจุดนี้ว่า P3' = (x, y) จากนั้นให้สะท้อนกับแกน x เพื่อได้ P3 = (x, -y)

มีกรณีพิเศษบางกรณีที่อธิบายความจำเป็นของ "จุดที่อนันต์":

ถ้า P1 และ P2 เป็นจุดเดียวกัน เส้น "ระหว่าง" P1 และ P2 ควรขยายเป็นเส้นสัมผัสกับเส้นโค้ง ณ จุด P1 นี้ เส้นสัมผัสนี้จะตัดกับเส้นโค้งที่จุดใหม่อีกหนึ่งจุดพอดี คุณสามารถใช้เทคนิคจากแคลคูลัสเพื่อหาความชันของเส้นสัมผัส เทคนิคเหล่านี้ใช้ได้อย่างน่าแปลกใจ แม้ว่าเราจะจำกัดความสนใจไว้ที่จุดบนเส้นโค้งที่มีพิกัดเป็นจำนวนเต็มเท่านั้น!
ในบางกรณี (เช่น ถ้า P1 และ P2 มีค่า x เดียวกันแต่ค่า y ต่างกัน) เส้นสัมผัสจะตั้งฉากพอดี ซึ่งในกรณีนี้ P3 = "จุดที่อนันต์"
ถ้า P1 เป็น "จุดที่อนันต์" แล้ว P1 + P2 = P2 ในทำนองเดียวกัน ถ้า P2 เป็นจุดที่อนันต์ แล้ว P1 + P2 = P1 นี่แสดงให้เห็นว่าจุดที่อนันต์มีบทบาทเป็นศูนย์

การบวกนี้มีคุณสมบัติเชิงสมาคม (associative) ซึ่งหมายความว่า (A + B) + C = A + (B + C) นั่นหมายความว่าเราสามารถเขียน A + B + C โดยไม่ต้องมีวงเล็บและไม่มีความกำกวม

เมื่อเรานิยามการบวกแล้ว เราสามารถนิยามการคูณในแบบมาตรฐานที่ต่อยอดจากการบวก สำหรับจุด P บนเส้นโค้งวงรี ถ้า k เป็นจำนวนเต็มบวก แล้ว kP = P + P + P + … + P (k ครั้ง) โปรดทราบว่า k บางครั้งถูกเรียกว่า "เลขชี้กำลัง"

Public Keys

ในระบบคริปโตกราฟีแบบเส้นโค้งวงรี (Elliptic Curve Cryptography) public key ถูกคำนวณจาก private key โดยใช้การคูณเส้นโค้งวงรี ซึ่งเป็นกระบวนการที่ไม่สามารถย้อนกลับได้:

K = k × G

โดยที่:

k คือ private key
G คือจุดคงที่ที่เรียกว่า จุดกำเนิด (generator point)
K คือ public key

การดำเนินการย้อนกลับ ที่เรียกว่า "การหาลอการิทึมแบบไม่ต่อเนื่อง" (finding the discrete logarithm) - คือการคำนวณหา k เมื่อรู้ค่า K - เป็นสิ่งที่ยากมากเทียบเท่ากับการลองค่า k ทุกค่าที่เป็นไปได้ (วิธีการแบบ brute-force)

ความยากของการย้อนกลับนี้คือหลักการความปลอดภัยหลักของระบบ ECC ที่ใช้ในบิตคอยน์ ซึ่งทำให้สามารถเผยแพร่ public key ได้อย่างปลอดภัย โดยที่ไม่ต้องกังวลว่าจะมีใครสามารถคำนวณย้อนกลับเพื่อหา private key ได้

TIP:การคูณเส้นโค้งวงรีเป็นฟังก์ชันประเภทที่นักเข้ารหัสลับเรียกว่า “ trap door function ”:

เป็นสิ่งที่ทำได้ง่ายในทิศทางหนึ่ง
แต่เป็นไปไม่ได้ที่จะทำในทิศทางตรงกันข้าม

คนที่มี private key สามารถสร้าง public key ได้อย่างง่ายดาย และสามารถแบ่งปันกับโลกได้โดยรู้ว่าไม่มีใครสามารถย้อนกลับฟังก์ชันและคำนวณ private key จาก public key ได้ กลวิธีทางคณิตศาสตร์นี้กลายเป็นพื้นฐานสำหรับลายเซ็นดิจิทัลที่ปลอมแปลงไม่ได้และมีความปลอดภัย ซึ่งใช้พิสูจน์การควบคุมเงินบิตคอยน์

เริ่มต้นด้วยการใช้ private key ในรูปแบบของตัวเลขสุ่ม เราคูณมันด้วยจุดที่กำหนดไว้ล่วงหน้าบนเส้นโค้งที่เรียกว่า จุดกำเนิด (generator point) เพื่อสร้างจุดอื่นที่อยู่บนเส้นโค้งเดียวกัน ซึ่งคำตอบจะเป็น public key ที่สอดคล้องกัน จุดกำเนิดถูกกำหนดไว้เป็นส่วนหนึ่งของมาตรฐาน secp256k1 และเป็นค่าเดียวกันสำหรับกุญแจทั้งหมดในระบบบิตคอยน์

เนื่องจากจุดกำเนิด G เป็นค่าเดียวกันสำหรับผู้ใช้บิตคอยน์ทุกคน private key (k) ที่คูณกับ G จะได้ public key (K) เดียวกันเสมอ ความสัมพันธ์ระหว่าง k และ K เป็นแบบตายตัวแต่สามารถคำนวณได้ในทิศทางเดียวเท่านั้น คือจาก k ไปยัง K นี่คือเหตุผลที่ public key ของบิตคอยน์ (K) สามารถแบ่งปันกับทุกคนได้โดยไม่เปิดเผย private key (k) ของผู้ใช้

TIP: private key สามารถแปลงเป็น public key ได้ แต่ public key ไม่สามารถแปลงกลับเป็น private key ได้ เพราะคณิตศาสตร์ที่ใช้ทำงานได้เพียงทิศทางเดียวเท่านั้น

เมื่อนำการคูณเส้นโค้งวงรีมาใช้งาน เราจะนำ private key (k) ที่สร้างขึ้นก่อนหน้านี้มาคูณกับจุดกำเนิด G เพื่อหา public key (K):

K = 1E99423A4ED27608A15A2616A2B0E9E52CED330AC530EDCC32C8FFC6A526AEDD × G

public key (K) จะถูกกำหนดเป็นจุด K = (x, y) โดยที่:

x = F028892BAD7ED57D2FB57BF33081D5CFCF6F9ED3D3D7F159C2E2FFF579DC341A
        y = 07CF33DA18BD734C600B96A72BBC4749D5141C90EC8AC328AE52DDFE2E505BDB

เพื่อจะให้เห็นภาพของการคูณจุดด้วยจำนวนเต็มมากขึ้น เราจะใช้เส้นโค้งวงรีที่ง่ายกว่าบนจำนวนจริง (โดยหลักการทางคณิตศาสตร์ยังคงเหมือนกัน) เป้าหมายของเราคือการหาผลคูณ kG ของจุดกำเนิด G ซึ่งเทียบเท่ากับการบวก G เข้ากับตัวเอง k ครั้งติดต่อกัน

ในเส้นโค้งวงรี การบวกจุดเข้ากับตัวเองเทียบเท่ากับการลากเส้นสัมผัสที่จุดนั้นและหาว่าเส้นนั้นตัดกับเส้นโค้งอีกครั้งที่จุดใด จากนั้นจึงสะท้อนจุดนั้นบนแกน x

การเข้ารหัสลับด้วยเส้นโค้งวงรี: การแสดงภาพการคูณจุด G ด้วยจำนวนเต็ม k บนเส้นโค้งวงรี แสดงกระบวนการในการหา G, 2G, 4G เป็นการดำเนินการทางเรขาคณิตบนเส้นโค้งได้ดังนี้

TIP: ในซอฟแวร์ของบิตคอยน์ส่วนใหญ่ใช้ไลบรารีเข้ารหัสลับ libsecp256k1 เพื่อทำการคำนวณทางคณิตศาสตร์เส้นโค้งวงรี

Output and Input Scripts

แม้ว่าภาพประกอบจาก Bitcoin whitepaper ที่แสดงเรื่อง "Transaction chain" จะแสดงให้เห็นว่ามีการใช้ public key และ digital signature โดยตรง แต่ในความเป็นจริงบิตคอยน์เวอร์ชันแรกนั้นมีการส่งการชำระเงินไปยังฟิลด์ที่เรียกว่า output script และมีการใช้จ่ายบิตคอยน์เหล่านั้นโดยได้รับอนุญาตจากฟิลด์ที่เรียกว่า input script ฟิลด์เหล่านี้อนุญาตให้มีการดำเนินการเพิ่มเติมนอกเหนือจาก (หรือแทนที่) การตรวจสอบว่าลายเซ็นสอดคล้องกับ public key หรือไม่ ตัวอย่างเช่น output script สามารถมี public key สองดอกและต้องการลายเซ็นสองลายเซ็นที่สอดคล้องกันในฟิลด์ input script ที่ใช้จ่าย

ในภายหลัง ในหัวข้อ [tx_script] เราจะได้เรียนรู้เกี่ยวกับสคริปต์อย่างละเอียด สำหรับตอนนี้ สิ่งที่เราต้องเข้าใจคือ บิตคอยน์จะถูกรับเข้า output script ที่ทำหน้าที่เหมือน public key และการใช้จ่ายบิตคอยน์จะได้รับอนุญาตโดย input script ที่ทำหน้าที่เหมือนลายเซ็น

IP Addresses: The Original Address for Bitcoin (P2PK)

เราได้เห็นแล้วว่าอลิซสามารถจ่ายเงินให้บ็อบโดยการมอบบิตคอยน์บางส่วนของเธอให้กับกุญแจสาธารณะของบ็อบ แต่อลิซจะได้กุญแจสาธารณะของบ็อบมาได้อย่างไร? บ็อบอาจจะให้สำเนากุญแจแก่เธอ แต่ลองดูกุญแจสาธารณะที่เราใช้งานในตัวอย่างที่ผ่านมาอีกครั้ง:

x = F028892BAD7ED57D2FB57BF33081D5CFCF6F9ED3D3D7F159C2E2FFF579DC341A
        y = 07CF33DA18BD734C600B96A72BBC4749D5141C90EC8AC328AE52DDFE2E505BDB

TIP จากหลาม: :สังเกตได้ว่า public key มีความยาวมาก ลองจินตนาการว่าบ็อบพยายามอ่านกุญแจนี้ให้อลิซฟังทางโทรศัพท์ คงจะยากมากที่จะอ่านและบันทึกโดยไม่มีข้อผิดพลาด

แทนที่จะป้อนกุญแจสาธารณะโดยตรง เวอร์ชันแรกของซอฟต์แวร์บิตคอยน์อนุญาตให้ผู้จ่ายเงินป้อนที่อยู่ IP ของผู้รับได้ ตามที่แสดงในหน้าจอการส่งเงินรุ่นแรกของบิตคอยน์ผ่าน The Internet Archive

คุณสมบัตินี้ถูกลบออกในภายหลัง เนื่องจากมีปัญหามากมายในการใช้ที่อยู่ IP แต่คำอธิบายสั้นๆ จะช่วยให้เราเข้าใจได้ดีขึ้นว่าทำไมคุณสมบัติบางอย่างอาจถูกเพิ่มเข้าไปในโปรโตคอลบิตคอยน์

เมื่ออลิซป้อนที่อยู่ IP ของบ็อบในบิตคอยน์เวอร์ชัน 0.1 Full node ของเธอจะทำการเชื่อมต่อกับ full node ของเขาและได้รับ public key ใหม่จากกระเป๋าสตางค์ของบ็อบที่โหนดของเขาไม่เคยให้กับใครมาก่อน การที่เป็น public key ใหม่นี้มีความสำคัญเพื่อให้แน่ใจว่าธุรกรรมต่าง ๆ ที่จ่ายให้บ็อบจะไม่สามารถถูกเชื่อมโยงเข้าด้วยกันโดยคนที่กำลังดูบล็อกเชนและสังเกตเห็นว่าธุรกรรมทั้งหมดจ่ายไปยัง public key เดียวกัน

เมื่อใช้ public key จากโหนดของอลิซซึ่งได้รับมาจากโหนดของบ็อบ กระเป๋าสตางค์ของอลิซจะสร้างเอาต์พุตธุรกรรมที่จ่ายให้กับสคริปต์เอาต์พุตดังนี้

<Bob's public key> OP_CHECKSIG

ต่อมาบ็อบจะสามารถใช้จ่ายเอาต์พุตนั้นด้วยสคริปต์อินพุตที่ประกอบด้วยลายเซ็นของเขาเท่านั้น:

<Bob's signature>

เพื่อให้เข้าใจว่าสคริปต์อินพุตและเอาต์พุตกำลังทำอะไร คุณสามารถรวมพวกมันเข้าด้วยกัน (สคริปต์อินพุตก่อน) แล้วสังเกตว่าข้อมูลแต่ละชิ้น (แสดงในเครื่องหมาย < >) จะถูกวางไว้ที่ด้านบนสุดของรายการที่เรียกว่าสแตก (stack) เมื่อพบรหัสคำสั่ง (opcode) มันจะใช้รายการจากสแตก โดยเริ่มจากรายการบนสุด มาดูว่ามันทำงานอย่างไรโดยเริ่มจากสคริปต์ที่รวมกัน:

<Bob's signature> <Bob's public key> OP_CHECKSIG

สำหรับสคริปต์นี้ ลายเซ็นของบ็อบจะถูกนำไปไว้บนสแตก จากนั้น public key ของบ็อบจะถูกวางไว้ด้านบนของลายเซ็น และบนสุดจะเป็นคำสั่ง OP_CHECKSIG ที่จะใช้องค์ประกอบสองอย่าง เริ่มจาก public key ตามด้วยลายเซ็น โดยลบพวกมันออกจากสแตก มันจะตรวจสอบว่าลายเซ็นตรงกับ public key และยืนยันฟิลด์ต่าง ๆ ในธุรกรรม ถ้าลายเซ็นถูกต้อง OP_CHECKSIG จะแทนที่ตัวเองบนสแตกด้วยค่า 1 ถ้าลายเซ็นไม่ถูกต้อง มันจะแทนที่ตัวเองด้วย 0 ถ้ามีรายการที่ไม่ใช่ศูนย์อยู่บนสุดของสแตกเมื่อสิ้นสุดการประเมิน สคริปต์ก็จะผ่าน ถ้าสคริปต์ทั้งหมดในธุรกรรมผ่าน และรายละเอียดอื่น ๆ ทั้งหมดเกี่ยวกับธุรกรรมนั้นต้องถูกต้องจึงจะถือว่าธุรกรรมนั้นถูกต้อง

โดยสรุป สคริปต์ข้างต้นใช้ public key และลายเซ็นเดียวกันกับที่อธิบายใน whitepaper แต่เพิ่มความซับซ้อนของฟิลด์สคริปต์สองฟิลด์และรหัสคำสั่งหนึ่งตัว ซึ่งเราจะเริ่มเห็นประโยชน์เมื่อเรามองที่ส่วนต่อไป

TIP:จากหลาม agian: เอาต์พุตประเภทนี้เป็นที่รู้จักในปัจจุบันว่า P2PK ซึ่งมันไม่เคยถูกใช้อย่างแพร่หลายสำหรับการชำระเงิน และไม่มีโปรแกรมที่ใช้กันอย่างแพร่หลายที่รองรับการชำระเงินผ่านที่อยู่ IP เป็นเวลาเกือบทศวรรษแล้ว

Legacy addresses for P2PKH

แน่นอนว่าการป้อนที่อยู่ IP ของคนที่คุณต้องการจ่ายเงินให้นั้นมีข้อดีหลายประการ แต่ก็มีข้อเสียหลายประการเช่นกัน หนึ่งในข้อเสียที่สำคัญคือผู้รับจำเป็นต้องให้กระเป๋าสตางค์ของพวกเขาออนไลน์ที่ที่อยู่ IP ของพวกเขา และต้องสามารถเข้าถึงได้จากโลกภายนอก

ซึ่งสำหรับคนจำนวนมากนั่นไม่ใช่ตัวเลือกที่เป็นไปได้เพราะหากพวกเขา:

ปิดคอมพิวเตอร์ในเวลากลางคืน
แล็ปท็อปของพวกเขาเข้าสู่โหมดสลีป
อยู่หลังไฟร์วอลล์
หรือกำลังใช้การแปลงที่อยู่เครือข่าย (NAT)

ปัญหานี้นำเรากลับมาสู่ความท้าทายเดิมที่ผู้รับเงินอย่างบ็อบต้องให้ public key ที่มีความยาวมากแก่ผู้จ่ายเงินอย่างอลิซ public key ของบิตคอยน์ที่สั้นที่สุดที่นักพัฒนาบิตคอยน์รุ่นแรกรู้จักมีขนาด 65 ไบต์ เทียบเท่ากับ 130 ตัวอักษรเมื่อเขียนในรูปแบบเลขฐานสิบหก (เฮกซาเดซิมอล) แต่อย่างไรก็ตาม บิตคอยน์มีโครงสร้างข้อมูลหลายอย่างที่มีขนาดใหญ่กว่า 65 ไบต์มาก ซึ่งจำเป็นต้องถูกอ้างอิงอย่างปลอดภัยในส่วนอื่น ๆ ของบิตคอยน์โดยใช้ข้อมูลขนาดเล็กที่สุดเท่าที่จะปลอดภัยได้

โดยบิตคอยน์แก้ปัญหานี้ด้วย ฟังก์ชันแฮช (hash function) ซึ่งเป็นฟังก์ชันที่รับข้อมูลที่อาจมีขนาดใหญ่ นำมาแฮช และให้ผลลัพธ์เป็นข้อมูลขนาดคงที่ ฟังก์ชันแฮชจะผลิตผลลัพธ์เดียวกันเสมอเมื่อได้รับข้อมูลนำเข้าแบบเดียวกัน และฟังก์ชันที่ปลอดภัยจะทำให้เป็นไปไม่ได้ในทางปฏิบัติสำหรับผู้ที่ต้องการเลือกข้อมูลนำเข้าอื่นที่ให้ผลลัพธ์เหมือนกันได้ นั่นทำให้ผลลัพธ์เป็น คำมั่นสัญญา (commitment) ต่อข้อมูลนำเข้า เป็นสัญญาว่าในทางปฏิบัติ มีเพียงข้อมูลนำเข้า x เท่านั้นที่จะให้ผลลัพธ์ X

สมมติว่าผมต้องการถามคำถามคุณและให้คำตอบของผมในรูปแบบที่คุณไม่สามารถอ่านได้ทันที สมมติว่าคำถามคือ "ในปีไหนที่ซาโตชิ นาคาโมโตะเริ่มทำงานบนบิทคอยน์?" ผมจะให้การยืนยันคำตอบของผมในรูปแบบของผลลัพธ์จากฟังก์ชันแฮช SHA256 ซึ่งเป็นฟังก์ชันที่ใช้บ่อยที่สุดในบิทคอยน์:

94d7a772612c8f2f2ec609d41f5bd3d04a5aa1dfe3582f04af517d396a302e4e

ต่อมา หลังจากคุณบอกคำตอบที่คุณเดาสำหรับคำถามนั้น ผมสามารถเปิดเผยคำตอบของผมและพิสูจน์ให้คุณเห็นว่าคำตอบของผม เมื่อใช้เป็นข้อมูลสำหรับฟังก์ชันแฮช จะให้ผลลัพธ์เดียวกันกับที่ผมให้คุณก่อนหน้านี้

$ echo "2007.  He said about a year and a half before Oct 2008" | sha256sum
        94d7a772612c8f2f2ec609d41f5bd3d04a5aa1dfe3582f04af517d396a302e4e

ทีนี้ให้สมมติว่าเราถามบ็อบว่า " public key ของคุณคืออะไร?" บ็อบสามารถใช้ฟังก์ชันแฮชเพื่อให้การยืนยันที่ปลอดภัยทางการเข้ารหัสต่อ public key ของเขา หากเขาเปิดเผยกุญแจในภายหลัง และเราตรวจสอบว่ามันให้ผลการยืนยันเดียวกันกับที่เขาให้เราก่อนหน้านี้ เราสามารถมั่นใจได้ว่ามันเป็นกุญแจเดียวกันที่ใช้สร้างการยืนยันก่อนหน้านี้

ฟังก์ชันแฮช SHA256 ถือว่าปลอดภัยมากและให้ผลลัพธ์ 256 บิต (32 ไบต์) น้อยกว่าครึ่งหนึ่งของขนาด public key ของบิทคอยน์ดั้งเดิม แต่อย่างไรก็ตาม มีฟังก์ชันแฮชอื่นๆ ที่ปลอดภัยน้อยกว่าเล็กน้อยที่ให้ผลลัพธ์ขนาดเล็กกว่า เช่น ฟังก์ชันแฮช RIPEMD-160 ซึ่งให้ผลลัพธ์ 160 บิต (20 ไบต์) ด้วยเหตุผลที่ซาโตชิ นาคาโมโตะไม่เคยระบุ เวอร์ชันดั้งเดิมของบิทคอยน์สร้างการยืนยันต่อ public key โดยการแฮชกุญแจด้วย SHA256 ก่อน แล้วแฮชผลลัพธ์นั้นด้วย RIPEMD-160 ซึ่งให้การยืนยันขนาด 20 ไบต์ต่อ public key

เราสามารถดูสิ่งนี้ตามอัลกอริทึม เริ่มจากกุญแจสาธารณะ K เราคำนวณแฮช SHA256 และคำนวณแฮช RIPEMD-160 ของผลลัพธ์ ซึ่งให้ตัวเลข 160 บิต (20 ไบต์): A = RIPEMD160(SHA256(K))

ทีนี้เราคงเข้าใจวิธีสร้างการยืนยันต่อ public key แล้ว ต่อไปเราจะมาดูวิธีการใช้งานโดยพิจารณาสคริปต์เอาต์พุตต่อไปนี้:

OP_DUP OP_HASH160 <Bob's commitment> OP_EQUAL OP_CHECKSIG

และสคริปต์อินพุตต่อไปนี้:

<Bob's signature> <Bob's public key>

และเมื่อเรารวมมันเข้าด้วยกันเราจะได้ผลลัพธ์ดังนี้:

<Bob's signature> <Bob's public key> OP_DUP OP_HASH160 <Bob's commitment> OP_EQUAL OP_CHECKSIG

เหมือนที่เราทำใน IP Addresses: The Original Address for Bitcoin (P2PK) เราเริ่มวางรายการลงในสแต็ก ลายเซ็นของบ็อบถูกวางก่อน จากนั้น public key ของเขาถูกวางไว้ด้านบน จากนั้นดำเนินการ OP_DUP เพื่อทำสำเนารายการบนสุด ดังนั้นรายการบนสุดและรายการที่สองจากบนในสแต็กตอนนี้เป็น public key ของบ็อบทั้งคู่ การดำเนินการ OP_HASH160 ใช้ (ลบ) public key บนสุดและแทนที่ด้วยผลลัพธ์ของการแฮชด้วย RIPEMD160(SHA256(K)) ดังนั้นตอนนี้บนสุดของสแต็กคือแฮชของ public key ของบ็อบ ต่อไป commitment ถูกเพิ่มไว้บนสุดของสแต็ก การดำเนินการ OP_EQUALVERIFY ใช้รายการสองรายการบนสุดและตรวจสอบว่าพวกมันเท่ากัน ซึ่งควรเป็นเช่นนั้นหาก public key ที่บ็อบให้ในสคริปต์อินพุตเป็น public key เดียวกันกับที่ใช้สร้างการยืนยันในสคริปต์เอาต์พุตที่อลิซจ่าย หาก OP_EQUALVERIFY ล้มเหลว ทั้งสคริปต์จะล้มเหลว สุดท้าย เราเหลือสแต็กที่มีเพียงลายเซ็นของบ็อบและ public key ของเขา รหัสปฏิบัติการ OP_CHECKSIG ตรวจสอบว่าพวกมันสอดคล้องกัน

TIP: จากหลาม ถ้าอ่านตรงนี้และงง ๆ ผมไปทำรูปมาให้ดูง่ายขึ้นครับ

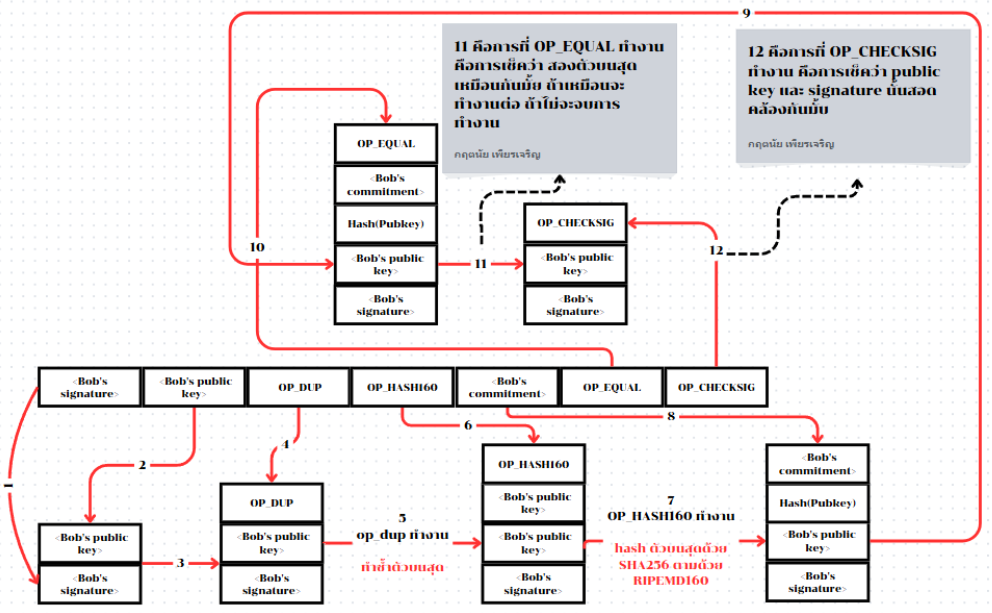
แม้กระบวนการของการ pay-to-publickey-hash(P2PKH) อาจดูซับซ้อน แต่มันทำให้การที่อลิซจ่ายเงินให้บ็อบมีเพียงการยืนยันเพียง 20 ไบต์ต่อ public key ของเขาแทนที่จะเป็นตัวกุญแจเอง ซึ่งจะมีขนาด 65 ไบต์ในเวอร์ชันดั้งเดิมของบิทคอยน์ นั่นเป็นข้อมูลที่น้อยกว่ามากที่บ็อบต้องสื่อสารกับอลิซ

แต่อย่างไรก็ตาม เรายังไม่ได้พูดถึงวิธีที่บ็อบรับ 20 ไบต์เหล่านั้นจากกระเป๋าเงินบิทคอยน์ของเขาไปยังกระเป๋าเงินของอลิซ มีการเข้ารหัสค่าไบต์ที่ใช้กันอย่างแพร่หลาย เช่น เลขฐานสิบหก แต่ข้อผิดพลาดใด ๆ ในการคัดลอกการยืนยันจะทำให้บิทคอยน์ถูกส่งไปยังเอาต์พุตที่ไม่สามารถใช้จ่ายได้ ทำให้พวกมันสูญหายไปตลอดกาล โดยในส่วนถัดไป เราจะดูที่การเข้ารหัสแบบกะทัดรัดและการตรวจสอบความถูกต้อง

Base58check Encoding

ระบบคอมพิวเตอร์มีวิธีเขียนตัวเลขยาวๆ ให้สั้นลงโดยใช้ทั้งตัวเลขและตัวอักษรผสมกัน เพื่อใช้พื้นที่น้อยลงอย่างเช่น

ระบบเลขฐานสิบ (ปกติที่เราใช้) - ใช้เลข 0-9 เท่านั้น
ระบบเลขฐานสิบหก - ใช้เลข 0-9 และตัวอักษร A-F ตัวอย่าง: เลข 255 ในระบบปกติ เขียนเป็น FF ในระบบเลขฐานสิบหก (สั้นกว่า)
ระบบเลขฐานหกสิบสี่ (Base64) - ใช้สัญลักษณ์ถึง 64 ตัว: ตัวอักษรเล็ก (a-z) 26 ตัว, ตัวอักษรใหญ่ (A-Z) 26 ตัว, ตัวเลข (0-9) 10 ตัว, สัญลักษณ์พิเศษอีก 2 ตัว ("+" และ "/")

โดยระบบ Base64 นี้ช่วยให้เราส่งไฟล์คอมพิวเตอร์ผ่านข้อความธรรมดาได้ เช่น การส่งรูปภาพผ่านอีเมล โดยใช้พื้นที่น้อยกว่าการเขียนเป็นเลขฐานสิบแบบปกติมาก

การเข้ารหัสแบบ Base58 คล้ายกับ Base64 โดยใช้ตัวอักษรพิมพ์ใหญ่ พิมพ์เล็ก และตัวเลข แต่ได้ตัดตัวอักษรบางตัวที่มักถูกเข้าใจผิดว่าเป็นตัวอื่นและอาจดูเหมือนกันเมื่อแสดงในฟอนต์บางประเภทออกไป

Base58 คือ Base64 ที่ตัดตัวอักษรต่อไปนี้ออก:

เลข 0 (ศูนย์)
ตัวอักษร O (ตัว O พิมพ์ใหญ่)
ตัวอักษร l (ตัว L พิมพ์เล็ก)
ตัวอักษร I (ตัว I พิมพ์ใหญ่)
และสัญลักษณ์ "+" และ "/"

หรือพูดให้ง่ายขึ้น Base58 คือกลุ่มตัวอักษรพิมพ์เล็ก พิมพ์ใหญ่ และตัวเลข แต่ไม่มีตัวอักษรทั้งสี่ตัว (0, O, l, I) ที่กล่าวถึงข้างต้น ตัวอักษรทั้งหมดที่ใช้ใน Base58 จะแสดงให้เห็นในตัวอักษร Base58 ของบิทคอยน์

Example 2. Bitcoin’s base58 alphabet

123456789ABCDEFGHJKLMNPQRSTUVWXYZabcdefghijkmnopqrstuvwxyz

การเพิ่มความปลอดภัยพิเศษเพื่อป้องกันการพิมพ์ผิดหรือข้อผิดพลาดในการคัดลอก base58check ได้รวม รหัสตรวจสอบ (checksum) ที่เข้ารหัสในตัวอักษร base58 เข้าไปด้วย รหัสตรวจสอบนี้คือข้อมูลเพิ่มเติมอีก 4 ไบต์ที่เพิ่มเข้าไปที่ท้ายของข้อมูลที่กำลังถูกเข้ารหัส

รหัสตรวจสอบนี้ได้มาจากการแฮชข้อมูลที่ถูกเข้ารหัส และจึงสามารถใช้เพื่อตรวจจับข้อผิดพลาดจากการคัดลอกและการพิมพ์ได้ เมื่อโปรแกรมได้รับรหัส base58check ซอฟต์แวร์ถอดรหัสจะคำนวณรหัสตรวจสอบของข้อมูลและเปรียบเทียบกับรหัสตรวจสอบที่รวมอยู่ในรหัสนั้น

หากทั้งสองไม่ตรงกัน แสดงว่ามีข้อผิดพลาดเกิดขึ้น และข้อมูล base58check นั้นไม่ถูกต้อง กระบวนการนี้ช่วยป้องกันไม่ให้ address บิทคอยน์ที่พิมพ์ผิดถูกยอมรับโดยซอฟต์แวร์กระเป๋าเงินว่าเป็น address ที่ถูกต้อง ซึ่งเป็นข้อผิดพลาดที่อาจส่งผลให้สูญเสียเงินได้

การแปลงข้อมูล (ตัวเลข) เป็นรูปแบบ base58check มีขั้นตอนดังนี้:

เราเริ่มโดยการเพิ่ม prefix เข้าไปในข้อมูล เรียกว่า "version byte" ซึ่งช่วยให้ระบุประเภทของข้อมูลที่ถูกเข้ารหัสได้ง่าย ตัวอย่างเช่น: prefix ศูนย์ (0x00 ในระบบเลขฐานสิบหก) แสดงว่าข้อมูลควรถูกใช้เป็นการยืนยัน (hash) ในสคริปต์เอาต์พุต legacy P2PKH
จากนั้น เราคำนวณ "double-SHA" checksum ซึ่งหมายถึงการใช้อัลกอริทึมแฮช SHA256 สองครั้งกับผลลัพธ์ก่อนหน้า (prefix ต่อกับข้อมูล):
```
checksum = SHA256(SHA256(prefix||data))
        
```
จากแฮช 32 ไบต์ที่ได้ (การแฮชซ้อนแฮช) เราเลือกเฉพาะ 4 ไบต์แรก ไบต์ทั้งสี่นี้ทำหน้าที่เป็นรหัสตรวจสอบข้อผิดพลาดหรือ checksum
นำ checksum นี้ไปต่อที่ท้ายข้อมูล

การเข้ารหัสแบบ base58check คือรูปแบบการเข้ารหัสที่ใช้ base58 พร้อมกับการระบุเวอร์ชันและการตรวจสอบความถูกต้อง เพื่อการเข้ารหัสข้อมูลบิทคอยน์ โดยคุณสามารถดูภาพประกอบด้านล่างเพื่อความเข้าใจเพิ่มเติม

ในบิตคอยน์นั้น นอกจากจะใช้ base58check ในการยืนยัน public key แล้ว ก็ยังมีการใช้ในข้อมูลอื่น ๆ ด้วย เพื่อทำให้ข้อมูลนั้นกะทัดรัด อ่านง่าย และตรวจจับข้อผิดพลาดได้ง่ายด้วยรหัสนำหน้า (version prefix) ในการเข้ารหัสแบบ base58check ถูกใช้เพื่อสร้างรูปแบบที่แยกแยะได้ง่าย ซึ่งเมื่อเข้ารหัสด้วย base58 โดยจะมีตัวอักษรเฉพาะที่จุดเริ่มต้นของข้อมูลที่เข้ารหัส base58check ตัวอักษรเหล่านี้ช่วยให้เราระบุประเภทของข้อมูลที่ถูกเข้ารหัสและวิธีการใช้งานได้ง่าย นี่คือสิ่งที่แยกความแตกต่าง ตัวอย่างเช่น ระหว่าง address บิทคอยน์ที่เข้ารหัส base58check ซึ่งขึ้นต้นด้วยเลข 1 กับรูปแบบการนำเข้า private key (WIF - Wallet Import Format) ที่เข้ารหัส base58check ซึ่งขึ้นต้นด้วยเลข 5 ตัวอย่างของ version prefix สามารถดูได้ตามตารางด้านล่างนี้

ภาพต่อไปนี้จะทำให้คุณเห็นภาพของกระบวนการแปลง public key ให้เป็น bitcoin address

Compressed Public Keys

ในยุคแรก ๆ ของบิตคอยน์นั้น มีเพียงการสร้าง public key แบบ 65 Bytes เท่านั้น แต่ในเวลาต่อมา เหล่านักพัฒนาในยุคหลังได้พบวิธีการสร้าง public key แบบใหม่ที่มีเพียง 33 Bytes และสามารถทำงานร่วมกันกับโหนดทั้งหมดในขณะนั้นได้ จีงไม่จะเป็นต้องเปลี่ยนแปลงกฎหรือโครงสร้างภายในโปรโตคอลของบิตคอยน์ โดย poublic key แบบใหม่ที่มีขนาด 33 Bytes นี้เรียกว่า compressed public key (public key ที่ถูกบีบอัด) และมีการเรียก public key ที่มีขนาด 65 Bytes ว่า uncompressed public key (public key ที่ไม่ถูกบีบอัด) ซึ่งประโยชน์ของ public key ที่เล็กลงนั้น นอกจากจะช่วยให้การส่ง public key ให้ผู้อื่นทำได้ง่ายขึ้นแล้ว ยังช่วยให้ธุรกรรมมีขนาดเล็กลง และช่วยให้สามารถทำการชำระเงินได้มากขึ้นในบล็อกเดียวกัน

อย่างที่เราได้เรียนรู้จากเนื้อหาในส่วนของ public key เราได้ทราบว่า public key คือจุด (x, y) บนเส้นโค้งวงรี เนื่องจากเส้นโค้งแสดงฟังก์ชันทางคณิตศาสตร์ จุดบนเส้นโค้งจึงเป็นคำตอบของสมการ ดังนั้นหากเรารู้พิกัด x เราก็สามารถคำนวณพิกัด y ได้โดยแก้สมการ y² mod p = (x³ + 7) mod p นั่นหมายความว่าเราสามารถเก็บเพียงพิกัด x ของ public key โดยละพิกัด y ไว้ ซึ่งช่วยลดขนาดของกุญแจและพื้นที่ที่ต้องใช้เก็บข้อมูลลง 256 บิต การลดขนาดลงเกือบ 50% ในทุกธุรกรรมรวมกันแล้วช่วยประหยัดข้อมูลได้มากมายในระยะยาว!

นี่คือ public key ที่ได้ยกเป็นตัวอย่างไว้ก่อนหน้า

x = F028892BAD7ED57D2FB57BF33081D5CFCF6F9ED3D3D7F159C2E2FFF579DC341A
        y = 07CF33DA18BD734C600B96A72BBC4749D5141C90EC8AC328AE52DDFE2E505BDB

และนี่คือ public key ที่มีตัวนำหน้า 04 ตามด้วยพิกัด x และ y ในรูปแบบ 04 x y:

K = 04F028892BAD7ED57D2FB57BF33081D5CFCF6F9ED3D3D7F159C2E2FFF579DC341A07CF33DA18BD734C600B96A72BBC4749D5141C90EC8AC328AE52DDFE2E505BDB

uncompressed public key นั้นจะมีตัวนำหน้าเป็น 04 แต่ compressed public key จะมีตัวนำหน้าเป็น 02 หรือ 03 โดยเหตุผลนั้นมาจากสมการ y² mod p = (x³ + 7) mod p เนื่องจากด้านซ้ายของสมการคือ y² คำตอบสำหรับ y จึงเป็นรากที่สอง ซึ่งอาจมีค่าเป็นบวกหรือลบก็ได้ หากมองเชิงภาพ นี่หมายความว่าพิกัด y ที่ได้อาจอยู่เหนือหรือใต้แกน x เราต้องไม่ลืมว่าเส้นโค้งมีความสมมาตร ซึ่งหมายความว่ามันจะสะท้อนเหมือนกระจกโดยแกน x ดังนั้น แม้เราจะละพิกัด y ได้ แต่เราต้องเก็บ เครื่องหมาย ของ y (บวกหรือลบ) หรืออีกนัยหนึ่งคือเราต้องจำว่ามันอยู่เหนือหรือใต้แกน x เพราะแต่ละตำแหน่งแทนจุดที่แตกต่างกันและเป็น public key ที่แตกต่างกัน

เมื่อคำนวณเส้นโค้งวงรีในระบบเลขฐานสองบนสนามจำกัดของเลขจำนวนเฉพาะ p พิกัด y จะเป็นเลขคู่หรือเลขคี่ ซึ่งสอดคล้องกับเครื่องหมายบวก/ลบตามที่อธิบายก่อนหน้านี้ ดังนั้น เพื่อแยกความแตกต่างระหว่างค่าที่เป็นไปได้สองค่าของ y เราจึงเก็บ compressed public key ด้วยตัวนำหน้า 02 ถ้า y เป็นเลขคู่ และ 03 ถ้า y เป็นเลขคี่ ซึ่งช่วยให้ซอฟต์แวร์สามารถอนุมานพิกัด y จากพิกัด x และคลายการบีบอัดของ public key ไปยังพิกัดเต็มของจุดได้อย่างถูกต้อง ดังภาพประกอบต่อไปนี้

นี่คือ public key เดียวกันกับที่ยกตัวอย่างไว้ข้างต้นซึ่งแสดงให้เห็นในรูป compressed public key ที่เก็บใน 264 บิต (66 ตัวอักษรเลขฐานสิบหก) โดยมีตัวนำหน้า 03 ซึ่งบ่งชี้ว่าพิกัด y เป็นเลขคี่:

K = 03F028892BAD7ED57D2FB57BF33081D5CFCF6F9ED3D3D7F159C2E2FFF579DC341A

compressed public key สอดคล้องกับ private key เดียวกันกับ uncompressed public key หมายความว่ามันถูกสร้างจาก private key เดียวกัน แต่อย่างไรก็ตาม มันก็มีส่วนที่แตกต่างจาก uncompressed public key นั้นคือ หากเราแปลง compressed public key เป็น commitment โดยใช้ฟังก์ชัน HASH160 (RIPEMD160(SHA256(K))) มันจะสร้าง commitment ที่แตกต่างจาก uncompressed public key และจะนำไปสู่ bitcoin address ที่แตกต่างกันในที่สุด สิ่งนี้อาจทำให้สับสนเพราะหมายความว่า private key เดียวสามารถสร้าง public key ในสองรูปแบบที่แตกต่างกัน (แบบบีบอัดและแบบไม่บีบอัด) ซึ่งสร้าง bitcoin address ที่แตกต่างกัน

compressed public key เป็นค่าเริ่มต้นในซอฟต์แวร์บิตคอยน์เกือบทั้งหมดในปัจจุบัน และถูกกำหนดให้ใช้กับคุณสมบัติใหม่บางอย่างที่เพิ่มในการอัปเกรดโปรโตคอลในภายหลัง

อย่างไรก็ตาม ซอฟต์แวร์บางตัวยังคงต้องรองรับ uncompressed public key เช่น แอปพลิเคชันกระเป๋าเงินที่นำเข้า private key จากกระเป๋าเงินเก่า เมื่อกระเป๋าเงินใหม่สแกนบล็อกเชนสำหรับผลลัพธ์และอินพุต P2PKH เก่า มันจำเป็นต้องรู้ว่าควรสแกนกุญแจขนาด 65 ไบต์ (และ commitment ของกุญแจเหล่านั้น) หรือกุญแจขนาด 33 ไบต์ (และ commitment ของกุญแจเหล่านั้น) หากไม่สแกนหาประเภทที่ถูกต้อง อาจทำให้ผู้ใช้ไม่สามารถใช้ยอดคงเหลือทั้งหมดได้ เพื่อแก้ไขปัญหานี้ เมื่อส่งออก private key จากกระเป๋าเงิน WIF ที่ใช้แสดง private key ในกระเป๋าเงินบิตคอยน์รุ่นใหม่จะถูกนำไปใช้แตกต่างกันเล็กน้อยเพื่อบ่งชี้ว่า private key เหล่านี้ถูกใช้ในการสร้าง compressed public key

Legacy: Pay to Script Hash (P2SH)

ตามที่เราได้เห็นในส่วนก่อนหน้านี้ ผู้รับบิตคอยน์ สามารถกำหนดให้การชำระเงินที่ส่งมาให้เขานั้นมีเงื่อนไขบางอย่างในสคริปต์เอาต์พุตได้โดยจะต้องปฏิบัติตามเงื่อนไขเหล่านั้นโดยใช้สคริปต์อินพุตเมื่อเขาใช้จ่ายบิตคอยน์เหล่านั้น ในส่วน IP Addresses: The Original Address for Bitcoin (P2PK) เงื่อนไขก็คือสคริปต์อินพุตต้องให้ลายเซ็นที่เหมาะสม ในส่วน Legacy Addresses for P2PKH นั้นจำเป็นต้องมี public key ที่เหมาะสมด้วย

ส่วนสำหรับผู้ส่งก็จะวางเงื่อนไขที่ผู้รับต้องการในสคริปต์เอาต์พุตที่ใช้จ่ายให้กับผู้รับ โดยผู้รับจะต้องสื่อสารเงื่อนไขเหล่านั้นให้ผู้ส่งทราบ ซึ่งคล้ายกับปัญหาที่บ๊อบต้องสื่อสาร public key ของเขาให้อลิซทราบ และเช่นเดียวกับปัญหานั้นที่ public key อาจมีขนาดค่อนข้างใหญ่ เงื่อนไขที่บ๊อบใช้ก็อาจมีขนาดใหญ่มากเช่นกัน—อาจมีขนาดหลายพันไบต์ นั่นไม่เพียงแต่เป็นข้อมูลหลายพันไบต์ที่ต้องสื่อสารให้อลิซทราบ แต่ยังเป็นข้อมูลหลายพันไบต์ที่เธอต้องจ่ายค่าธรรมเนียมธุรกรรมทุกครั้งที่ต้องการใช้จ่ายเงินให้บ๊อบ อย่างไรก็ตาม การใช้ฟังก์ชันแฮชเพื่อสร้าง commitment ขนาดเล็กสำหรับข้อมูลขนาดใหญ่ก็สามารถนำมาใช้ได้ในกรณีนี้เช่นกัน

ในเวลาต่อมานั้น การอัปเกรด BIP16 สำหรับโปรโตคอลบิตคอยน์ในปี 2012 ได้อนุญาตให้สคริปต์เอาต์พุตสร้าง commitment กับ redemption script (redeem script) ได้ แปลว่าเมื่อบ๊อบใช้จ่ายบิตคอยน์ของเขา ภายในสคริปต์อินพุตของเขานั้นจะต้องให้ redeem script ที่ตรงกับ commitment และข้อมูลที่จำเป็นเพื่อให้เป็นไปตาม redeem script (เช่น ลายเซ็น) เริ่มต้นด้วยการจินตนาการว่าบ๊อบต้องการให้มีลายเซ็นสองอันเพื่อใช้จ่ายบิตคอยน์ของเขา หนึ่งลายเซ็นจากกระเป๋าเงินบนเดสก์ท็อปและอีกหนึ่งจากอุปกรณ์เซ็นแบบฮาร์ดแวร์ เขาใส่เงื่อนไขเหล่านั้นลงใน redeem script:

<public key 1> OP_CHECKSIGVERIFY <public key 2> OP_CHECKSIG

จากนั้นเขาสร้าง commitment กับ redeem script โดยใช้กลไก HASH160 เดียวกับที่ใช้สำหรับ commitment แบบ P2PKH, RIPEMD160(SHA256(script)) commitment นั้นถูกวางไว้ในสคริปต์เอาต์พุตโดยใช้เทมเพลตพิเศษ:

OP_HASH160 <commitment> OP_EQUAL

คำเตือน: เมื่อใช้ pay to script hash (P2SH) คุณต้องใช้เทมเพลต P2SH โดยเฉพาะ ซึ่งจะไม่มีข้อมูลหรือเงื่อนไขเพิ่มเติมในสคริปต์เอาต์พุต หากสคริปต์เอาต์พุตไม่ได้เป็น OP_HASH160 <20 ไบต์> OP_EQUAL แน่นอนว่า redeem script จะไม่ถูกใช้และบิตคอยน์ใด ๆ อาจไม่สามารถใช้จ่ายได้หรืออาจถูกใช้จ่ายได้โดยทุกคน (หมายความว่าใครก็สามารถนำไปใช้ได้)

เมื่อบ๊อบต้องการจ่ายเงินที่เขาได้รับผ่าน commitment สำหรับสคริปต์ของเขา เขาจะใช้สคริปต์อินพุตที่รวมถึง redeem script ซึ่งถูกแปลงให้เป็นข้อมูลอีลิเมนต์เดียว นอกจากนี้เขายังให้ลายเซ็นที่จำเป็นเพื่อให้เป็นไปตาม redeem script โดยเรียงลำดับตามที่จะถูกใช้โดย opcodes:

<signature2> <signature1> <redeem script>

เมื่อโหนดของบิตคอยน์ได้รับการใช้จ่ายของบ๊อบพวกมันจะตรวจสอบว่า redeem script ที่ถูกแปลงเป็นค่าแฮชแล้วมีค่าเดียวกันกับ commitment มั้ย หลังจากนั้นพวกมันจะแทนที่มันบนสแต็คด้วยค่าที่ถอดรหัสแล้ว:

<signature2> <signature1> <pubkey1> OP_CHECKSIGVERIFY <pubkey2> OP_CHECKSIG

สคริปต์จะถูกประมวลผล และหากผ่านการตรวจสอบและรายละเอียดธุรกรรมอื่น ๆ ทั้งหมดถูกต้อง ธุรกรรมก็จะถือว่าใช้ได้

address สำหรับ P2SH ก็ถูกสร้างด้วย base58check เช่นกัน คำนำหน้าเวอร์ชันถูกตั้งเป็น 5 ซึ่งทำให้ที่อยู่ที่เข้ารหัสแล้วขึ้นต้นด้วยเลข 3 ตัวอย่างของที่อยู่ P2SH คือ 3F6i6kwkevjR7AsAd4te2YB2zZyASEm1HM

TIP: P2SH ไม่จำเป็นต้องเหมือนกับธุรกรรมแบบหลายลายเซ็น (multisignature) เสมอไป ถึง address P2SH ส่วนใหญ่ แทนสคริปต์แบบหลายลายเซ็นก็ตาม แต่อาจแทนสคริปต์ที่เข้ารหัสธุรกรรมประเภทอื่น ๆ ได้ด้วย

P2PKH และ P2SH เป็นสองเทมเพลตสคริปต์เท่านั้นที่ใช้กับการเข้ารหัสแบบ base58check พวกมันเป็นที่รู้จักในปัจจุบันว่าเป็น address แบบ legacy และกลายเป็นรูปแบบที่พบน้อยลงเรื่อยๆ address แบบ legacy ถูกแทนที่ด้วยaddress ตระกูล bech32

การโจมตี P2SH แบบ Collision

address ทั้งหมดที่อิงกับฟังก์ชันแฮชมีความเสี่ยงในทางทฤษฎีต่อผู้โจมตีที่อาจค้นพบอินพุตเดียวกันที่สร้างเอาต์พุตฟังก์ชันแฮช (commitment) โดยอิสระ ในกรณีของบิตคอยน์ หากพวกเขาค้นพบอินพุตในวิธีเดียวกับที่ผู้ใช้ดั้งเดิมทำ พวกเขาจะรู้ private key ของผู้ใช้และสามารถใช้จ่ายบิตคอยน์ของผู้ใช้นั้นได้ โอกาสที่ผู้โจมตีจะสร้างอินพุตสำหรับ commitment ที่มีอยู่แล้วโดยอิสระนั้นขึ้นอยู่กับความแข็งแกร่งของอัลกอริทึมแฮช สำหรับอัลกอริทึมที่ปลอดภัย 160 บิตอย่าง HASH160 ความน่าจะเป็นอยู่ที่ 1 ใน 2^160 นี่เรียกว่าการโจมตีแบบ preimage attack

ผู้โจมตีสามารถพยายามสร้างข้อมูลนำเข้าสองชุดที่แตกต่างกัน (เช่น redeem scripts) ที่สร้างการเข้ารหัสแบบเดียวกันได้ สำหรับ address ที่สร้างโดยฝ่ายเดียวทั้งหมด โอกาสที่ผู้โจมตีจะสร้างข้อมูลนำเข้าที่แตกต่างสำหรับการเข้ารหัสที่มีอยู่แล้วมีประมาณ 1 ใน 2^160 สำหรับอัลกอริทึม HASH160 นี่คือการโจมตีแบบ second preimage attack

อย่างไรก็ตาม สถานการณ์จะเปลี่ยนไปเมื่อผู้โจมตีสามารถมีอิทธิพลต่อค่าข้อมูลนำเข้าดั้งเดิมได้ ตัวอย่างเช่น ผู้โจมตีมีส่วนร่วมในการสร้างสคริปต์แบบหลายลายเซ็น (multisignature script) ซึ่งพวกเขาไม่จำเป็นต้องส่ง public key ของตนจนกว่าจะทราบ public key ของฝ่ายอื่นทั้งหมด ในกรณีนั้น ความแข็งแกร่งของอัลกอริทึมการแฮชจะลดลงเหลือรากที่สองของมัน สำหรับ HASH160 ความน่าจะเป็นจะกลายเป็น 1 ใน 2^80 นี่คือการโจมตีแบบ collision attack

เพื่อให้เข้าใจตัวเลขเหล่านี้ในบริบทที่ชัดเจน ข้อมูล ณ ต้นปี 2023 นักขุดบิตคอยน์ทั้งหมดรวมกันสามารถประมวลผลฟังก์ชันแฮชประมาณ 2^80 ทุกชั่วโมง พวกเขาใช้ฟังก์ชันแฮชที่แตกต่างจาก HASH160 ดังนั้นฮาร์ดแวร์ที่มีอยู่จึงไม่สามารถสร้างการโจมตีแบบ collision attack สำหรับมันได้ แต่การมีอยู่ของเครือข่ายบิตคอยน์พิสูจน์ว่าการโจมตีแบบชนกันต่อฟังก์ชัน 160 บิตอย่าง HASH160 สามารถทำได้จริงในทางปฏิบัติ นักขุดบิตคอยน์ได้ลงทุนเทียบเท่ากับหลายพันล้านดอลลาร์สหรัฐในฮาร์ดแวร์พิเศษ ดังนั้นการสร้างการโจมตีแบบ collision attack จึงไม่ใช่เรื่องถูก แต่มีองค์กรที่คาดหวังว่าจะได้รับบิตคอยน์มูลค่าหลายพันล้านดอลลาร์ไปยัง address ที่สร้างโดยกระบวนการที่เกี่ยวข้องกับหลายฝ่าย ซึ่งอาจทำให้การโจมตีนี้มีกำไร

มีโปรโตคอลการเข้ารหัสที่เป็นที่ยอมรับอย่างดีในการป้องกันการโจมตีแบบ collision attack แต่วิธีแก้ปัญหาที่ง่ายโดยไม่ต้องใช้ความรู้พิเศษจากผู้พัฒนากระเป๋าเงินคือการใช้ฟังก์ชันแฮชที่แข็งแกร่งกว่า การอัปเกรดบิตคอยน์ในภายหลังทำให้เป็นไปได้ และ address บิตคอยน์ใหม่ให้ความต้านทานการชนกันอย่างน้อย 128 บิต การดำเนินการแฮช 2^128 ครั้งจะใช้เวลานักขุดบิตคอยน์ปัจจุบันทั้งหมดประมาณ 32 พันล้านปี

แม้ว่าเราไม่เชื่อว่ามีภัยคุกคามเร่งด่วนต่อผู้ที่สร้าง address P2SH ใหม่ แต่เราแนะนำให้กระเป๋าเงินใหม่ทั้งหมดใช้ที่อยู่ประเภทใหม่เพื่อขจัดความกังวลเกี่ยวกับการโจมตีแบบ collision attack ของ P2SH address

Bech32 Addresses

ในปี 2017 โปรโตคอลบิตคอยน์ได้รับการอัปเกรด เพื่อป้องกันไม่ให้ตัวระบุธุรกรรม (txids) ไม่สามารถเปลี่ยนแปลงได้ โดยไม่ได้รับความยินยอมจากผู้ใช้ที่ทำการใช้จ่าย (หรือองค์ประชุมของผู้ลงนามเมื่อต้องมีลายเซ็นหลายรายการ) การอัปเกรดนี้เรียกว่า segregated witness (หรือเรียกสั้นๆ ว่า segwit) ซึ่งยังให้ความสามารถเพิ่มเติมสำหรับข้อมูลธุรกรรมในบล็อกและประโยชน์อื่น ๆ อีกหลายประการ แต่อย่างไรก็ตาม หากมีผู้ใช้เก่าที่ต้องการเข้าถึงประโยชน์ของ segwit โดยตรงต้องยอมรับการชำระเงินไปยังสคริปต์เอาต์พุตใหม่

ตามที่ได้กล่าวไว้ใน p2sh หนึ่งในข้อดีของเอาต์พุตประเภท P2SH คือผู้จ่ายไม่จำเป็นต้องรู้รายละเอียดของสคริปต์ที่ผู้รับใช้ การอัปเกรด segwit ถูกออกแบบมาให้ใช้กลไกนี้ได้ดังเดิม จึง ทำให้ผู้จ่ายสามารถเริ่มเข้าถึงประโยชน์ใหม่ ๆ หลายอย่างได้ทันทีโดยใช้ที่อยู่ P2SH แต่เพื่อให้ผู้รับสามารถเข้าถึงประโยชน์เหล่านั้นได้ พวกเขาจำเป็นจะต้องให้กระเป๋าเงินของผู้จ่ายจ่ายเงินให้เขาโดยใช้สคริปต์ประเภทอื่นแทน ซึ่งจะต้องอาศัยการอัปเกรดกระเป๋าเงินของผู้จ่ายเพื่อรองรับสคริปต์ใหม่เหล่านี้

ในช่วงแรก เหล่านักพัฒนาบิตคอยน์ได้นำเสนอ BIP142 ซึ่งจะยังคงใช้ base58check ร่วมกับไบต์เวอร์ชันใหม่ คล้ายกับการอัปเกรด P2SH แต่การให้กระเป๋าเงินทั้งหมดอัปเกรดไปใช้สคริปต์ใหม่ที่มีเวอร์ชัน base58check ใหม่นั้น คาดว่าจะต้องใช้ความพยายามเกือบเท่ากับการให้พวกเขาอัปเกรดไปใช้รูปแบบ address ที่เป็นแบบใหม่ทั้งหมด ด้วยเหตุนี้้เอง ผู้สนับสนุนบิตคอยน์หลายคนจึงเริ่มออกแบบรูปแบบ address ที่ดีที่สุดเท่าที่เป็นไปได้ พวกเขาระบุปัญหาหลายอย่างกับ base58check ไว้ดังนี้:

การที่ base58check ใช้อักษรที่มีทั้งตัวพิมพ์ใหญ่และตัวพิมพ์เล็กทำให้ไม่สะดวกในการอ่านออกเสียงหรือคัดลอก ลองอ่าน address แบบเก่าในบทนี้ให้เพื่อนฟังและให้พวกเขาคัดลอก คุณจะสังเกตว่าคุณต้องระบุคำนำหน้าทุกตัวอักษรด้วยคำว่า "ตัวพิมพ์ใหญ่" และ "ตัวพิมพ์เล็ก" และเมื่อคุณตรวจสอบสิ่งที่พวกเขาเขียน คุณจะพบว่าตัวพิมพ์ใหญ่และตัวพิมพ์เล็กของตัวอักษรบางตัวอาจดูคล้ายกันในลายมือของคนส่วนใหญ่
รูปแบบนี้สามารถตรวจจับข้อผิดพลาดได้ แต่ไม่สามารถช่วยผู้ใช้แก้ไขข้อผิดพลาดเหล่านั้น ตัวอย่างเช่น หากคุณสลับตำแหน่งตัวอักษรสองตัวโดยไม่ตั้งใจเมื่อป้อน address ด้วยตนเอง กระเป๋าเงินของคุณจะเตือนว่ามีข้อผิดพลาดเกิดขึ้นแน่นอน แต่จะไม่ช่วยให้คุณค้นพบว่าข้อผิดพลาดอยู่ที่ไหน คุณอาจต้องใช้เวลาหลายนาทีที่น่าหงุดหงิดเพื่อค้นหาข้อผิดพลาดในที่สุด
การใช้ตัวอักษรที่มีทั้งตัวพิมพ์ใหญ่และตัวพิมพ์เล็กยังต้องใช้พื้นที่เพิ่มเติมในการเข้ารหัสใน QR code ซึ่งนิยมใช้ในการแชร์ address และ invoice ระหว่างกระเป๋าเงิน พื้นที่เพิ่มเติมนี้หมายความว่า QR code จำเป็นต้องมีขนาดใหญ่ขึ้นที่ความละเอียดเดียวกัน หรือไม่เช่นนั้นก็จะยากต่อการสแกนอย่างรวดเร็ว
การที่ต้องการให้กระเป๋าเงินผู้จ่ายทุกใบอัปเกรดเพื่อรองรับคุณสมบัติโปรโตคอลใหม่ เช่น P2SH และ segwit แม้ว่าการอัปเกรดเองอาจไม่ต้องใช้โค้ดมากนัก แต่ประสบการณ์แสดงให้เห็นว่าผู้พัฒนากระเป๋าเงินหลายรายมักยุ่งกับงานอื่น ๆ และบางครั้งอาจล่าช้าในการอัปเกรดเป็นเวลาหลายปี สิ่งนี้ส่งผลเสียต่อทุกคนที่ต้องการใช้คุณสมบัติใหม่ ๆ เหล่านี้

นักพัฒนาที่ทำงานเกี่ยวกับรูปแบบ address สำหรับ segwit ได้พบวิธีแก้ปัญหาเหล่านี้ทั้งหมดในรูปแบบ address แบบใหม่ที่เรียกว่า bech32 (ออกเสียงด้วย "ch" อ่อน เช่นใน "เบช สามสิบสอง") คำว่า "bech" มาจาก BCH ซึ่งเป็นอักษรย่อของบุคคลสามคนที่ค้นพบรหัสวนนี้ในปี 1959 และ 1960 ซึ่งเป็นพื้นฐานของ bech32 ส่วน "32" หมายถึงจำนวนตัวอักษรในชุดตัวอักษร bech32 (คล้ายกับ 58 ใน base58check):

Bech32 ใช้เฉพาะตัวเลขและตัวอักษรรูปแบบเดียว (โดยปกติจะแสดงเป็นตัวพิมพ์เล็ก) แม้ว่าชุดตัวอักษรของมันจะมีขนาดเกือบครึ่งหนึ่งของชุดตัวอักษรใน base58check ก็ตามแต่ address bech32 สำหรับสคริปต์ pay to witness public key hash (P2WPKH) ก็ยังยาวกว่า legacy address และมีขนาดเท่ากันกับสคริปต์ P2PKH
Bech32 สามารถทั้งตรวจจับและช่วยแก้ไขข้อผิดพลาดได้ ใน address ที่มีความยาวตามที่คาดหวังได้ และสามารถรับประกันทางคณิตศาสตร์ได้ว่าจะตรวจพบข้อผิดพลาดใด ๆ ที่ส่งผลกระทบต่อตัวอักษร 4 ตัวหรือน้อยกว่า ซึ่งเชื่อถือได้มากกว่า base58check ส่วนสำหรับข้อผิดพลาดที่ยาวกว่านั้น จะไม่สามารถตรวจพบได้ (โอกาสเกิดน้อยกว่าหนึ่งครั้งในหนึ่งพันล้าน) ซึ่งมีความเชื่อถือได้ประมาณเท่ากับ base58check ยิ่งไปกว่านั้น สำหรับ adddress ที่พิมพ์โดยมีข้อผิดพลาดเพียงเล็กน้อย มันสามารถบอกผู้ใช้ได้ว่าข้อผิดพลาดเหล่านั้นเกิดขึ้นที่ไหน ช่วยให้พวกเขาสามารถแก้ไขข้อผิดพลาดจากการคัดลอกเล็ก ๆ น้อย ๆ ได้อย่างรวดเร็ว
ตัวอย่างที่ 3 Bech32 address ที่มีข้อผิดพลาด
Address: bc1p9nh05ha8wrljf7ru236awn4t2x0d5ctkkywmv9sclnm4t0av2vgs4k3au7
ข้อผิดพลาดที่ตรวจพบแสดงเป็นตัวหนาและขีดเส้นใต้ สร้างโดยใช้โปรแกรมสาธิตการถอดรหัส bech32 address
bech32 address นิยมเขียนด้วยตัวอักษรพิมพ์เล็กเท่านั้น แต่ตัวอักษรพิมพ์เล็กเหล่านี้สามารถแทนที่ด้วยตัวอักษรพิมพ์ใหญ่ก่อนการเข้ารหัส address ในรหัส QR ได้ วิธีนี้ช่วยให้สามารถใช้โหมดการเข้ารหัส QR แบบพิเศษที่ใช้พื้นที่น้อยกว่า คุณจะสังเกตเห็นความแตกต่างในขนาดและความซับซ้อนของรหัส QR ทั้งสองสำหรับที่อยู่เดียวกันในรูปภาพข้างล่างนี้

Bech32 ใช้ประโยชน์จากกลไกการอัปเกรดที่ออกแบบมาเป็นส่วนหนึ่งของ segwit เพื่อทำให้กระเป๋าเงินผู้จ่ายสามารถจ่ายเงินไปยังประเภทเอาต์พุตที่ยังไม่ได้ใช้งานได้ โดยมีเป้าหมายคือการอนุญาตให้นักพัฒนาสร้างกระเป๋าเงินในวันนี้ที่สามารถใช้จ่ายไปยัง bech32 address และทำให้กระเป๋าเงินนั้นยังคงสามารถใช้จ่ายไปยัง bech32address ได้สำหรับผู้ใช้คุณสมบัติใหม่ที่เพิ่มในการอัปเกรดโปรโตคอลในอนาคต โดยที่มีความหวังว่าเราอาจไม่จำเป็นต้องผ่านรอบการอัปเกรดทั้งระบบอีกต่อไป ซึ่งจำเป็นสำหรับการให้ผู้คนใช้งาน P2SH และ segwit ได้อย่างเต็มรูปแบบ
Problems with Bech32 Addresses

address แบบ bech32 ประสบความสำเร็จในทุกด้านยกเว้นปัญหาหนึ่ง คือการรับประกันทางคณิตศาสตร์เกี่ยวกับความสามารถในการตรวจจับข้อผิดพลาดจะใช้ได้เฉพาะเมื่อความยาวของ address ที่คุณป้อนเข้าไปในกระเป๋าเงินมีความยาวเท่ากับ address ดั้งเดิมเท่านั้น หากคุณเพิ่มหรือลบตัวอักษรใด ๆ ระหว่างการคัดลอกจะทำให้ไม่สามารถตรวจจับได้ การรับประกันนี้จะไม่มีผล และกระเป๋าเงินของคุณอาจใช้จ่ายเงินไปยัง address ที่ไม่ถูกต้อง แต่อย่างไรก็ตาม แม้จะไม่มีคุณสมบัตินี้ มีความเชื่อว่าเป็นไปได้ยากมากที่ผู้ใช้ที่เพิ่มหรือลบตัวอักษรจะสร้างสตริงที่มีผลรวมตรวจสอบที่ถูกต้อง ซึ่งช่วยให้มั่นใจได้ว่าเงินของผู้ใช้จะปลอดภัย

น่าเสียดายที่การเลือกใช้ค่าคงที่ตัวหนึ่งในอัลกอริทึม bech32 บังเอิญทำให้การเพิ่มหรือลบตัวอักษร "q" ในตำแหน่งที่สองจากท้ายของ address ที่ลงท้ายด้วยตัวอักษร "p" เป็นเรื่องง่ายมาก ในกรณีเหล่านั้น คุณยังสามารถเพิ่มหรือลบตัวอักษร "q" หลายครั้งได้ด้วย ข้อผิดพลาดนี้จะถูกตรวจจับโดยผลรวมตรวจสอบ (checksum) ในบางครั้ง แต่จะถูกมองข้ามบ่อยกว่าความคาดหวังหนึ่งในพันล้านสำหรับข้อผิดพลาดจากการแทนที่ของ bech32 อย่างมาก สำหรับตัวอย่างสามารถดูได้ในรูปภาพข้างล่างนี้

ตัวอย่างที่ 4. การขยายความยาวของ bech32 address โดยไม่ทำให้ผลรวมตรวจสอบเป็นโมฆะ

bech32 address ที่ถูกต้อง:
        bc1pqqqsq9txsqp
        
        address ที่ไม่ถูกต้องแต่มีผลรวมตรวจสอบที่ถูกต้อง:
        bc1pqqqsq9txsqqqqp
        bc1pqqqsq9txsqqqqqqp
        bc1pqqqsq9txsqqqqqqqqp
        bc1pqqqsq9txsqqqqqqqqqp
        bc1pqqqsq9txsqqqqqqqqqqqp

จากตัวอย่างนี้ คุณจะเห็นว่าแม้มีการเพิ่มตัวอักษร "q" เข้าไปหลายตัวก่อนตัวอักษร "p" ตัวสุดท้าย ระบบตรวจสอบก็ยังคงยอมรับว่า address เหล่านี้ถูกต้อง นี่เป็นข้อบกพร่องสำคัญของ bech32 เพราะอาจทำให้เงินถูกส่งไปยัง address ที่ไม่มีใครเป็นเจ้าของจริง ๆ หรือ address ที่ไม่ได้ตั้งใจจะส่งไป

สำหรับเวอร์ชันเริ่มต้นของ segwit (เวอร์ชัน 0) ปัญหานี้ไม่ใช่ความกังวลในทางปฏิบัติ เพราะมีความยาวที่ถูกต้องมีเพียงสองแบบที่กำหนดไว้สำหรับเอาต์พุต นั้นคือ 22 Byte และ 34 Byte ซึ่งสอดคล้องกับ bech32 address ที่มีความยาวยาวที่ 42 หรือ 62 ตัวอักษร ดังนั้นคนจะต้องเพิ่มหรือลบตัวอักษร "q" จากตำแหน่งที่สองจากท้ายของ bech32 address ถึง 20 ครั้งเพื่อส่งเงินไปยัง address ที่ไม่ถูกต้องโดยที่กระเป๋าเงินไม่สามารถตรวจจับได้ อย่างไรก็ตาม มันอาจกลายเป็นปัญหาสำหรับผู้ใช้ในอนาคตหากมีการนำการอัปเกรดบนพื้นฐานของ segwit มาใช้

Bech32m

แม้ว่า bech32 จะทำงานได้ดีสำหรับ segwit v0 แต่นักพัฒนาไม่ต้องการจำกัดขนาดเอาต์พุตโดยไม่จำเป็นในเวอร์ชันหลังๆ ของ segwit หากไม่มีข้อจำกัด การเพิ่มหรือลบตัวอักษร "q" เพียงตัวเดียวใน bech32 address อาจทำให้ผู้ใช้ส่งเงินโดยไม่ตั้งใจไปยังเอาต์พุตที่ไม่สามารถใช้จ่ายได้หรือสามารถใช้จ่ายได้โดยทุกคน (ทำให้บิตคอยน์เหล่านั้นถูกนำไปโดยทุกคนได้) นักพัฒนาได้วิเคราะห์ปัญหา bech32 อย่างละเอียดและพบว่าการเปลี่ยนค่าคงที่เพียงตัวเดียวในอัลกอริทึมของพวกเขาจะขจัดปัญหานี้ได้ ทำให้มั่นใจว่าการแทรกหรือลบตัวอักษรสูงสุดห้าตัวจะไม่ถูกตรวจจับน้อยกว่าหนึ่งครั้งในหนึ่งพันล้านเท่านั้น

เวอร์ชันของ bech32 ที่มีค่าคงที่เพียงหนึ่งตัวที่แตกต่างกันเรียกว่า bech32 แบบปรับแต่ง (bech32m) ตัวอักษรทั้งหมดใน address แบบ bech32 และ bech32m สำหรับข้อมูลพื้นฐานเดียวกันจะเหมือนกันทั้งหมด ยกเว้นหกตัวสุดท้าย (ซึ่งเป็นส่วนของ checksum) นั่นหมายความว่ากระเป๋าเงินจำเป็นต้องรู้ว่ากำลังใช้เวอร์ชันใดเพื่อตรวจสอบความถูกต้องของ checksum แต่ address ทั้งสองประเภทมีไบต์เวอร์ชันภายในที่ทำให้การระบุเวอร์ชันที่ใช้อยู่เป็นเรื่องที่ง่าย
ในการทำงานกับทั้ง bech32 และ bech32m เราจะพิจารณากฎการเข้ารหัสและการแยกวิเคราะห์สำหรับ address บิตคอยน์แบบ bech32m เนื่องจากพวกมันครอบคลุมความสามารถในการแยกวิเคราะห์บน address แบบ bech32 และเป็นรูปแบบ address ที่แนะนำในปัจจุบันสำหรับกระเป๋าเงินบิตคอยน์

ข้อความจากหลาม: คือผมว่าตรงนี้เขาเขียนไม่รู้เรื่อง แต่เดาว่าเขาน่าจะสื่อว่า เราควรเรียนรู้วิธีการทำงานกับ bech32m เพราะมันเป็นรูปแบบที่แนะนำให้ใช้ในปัจจุบัน และมันมีข้อดีเพราะbech32m สามารถรองรับการอ่าน address แบบ bech32 แบบเก่าได้ด้วย ง่ายๆ คือ ถ้าคุณเรียนรู้วิธีทำงานกับ bech32m คุณจะสามารถทำงานกับทั้ง bech32m และ bech32 ได้ทั้งสองแบบ

bech32m address ริ่มต้นด้วยส่วนที่มนุษย์อ่านได้ (Human Readable Part: HRP) BIP173 มีกฎสำหรับการสร้าง HRP ของคุณเอง แต่สำหรับบิตคอยน์ คุณเพียงแค่จำเป็นต้องรู้จัก HRP ที่ถูกเลือกไว้แล้วตามที่แสดงในตารางข้างล่างนี้

ส่วน HRP ตามด้วยตัวคั่น ซึ่งก็คือเลข "1" ในข้อเสนอก่อนหน้านี้สำหรับตัวคั่นโปรโตคอลได้ใช้เครื่องหมายทวิภาค (colon) แต่ระบบปฏิบัติการและแอปพลิเคชันบางตัวที่อนุญาตให้ผู้ใช้ดับเบิลคลิกคำเพื่อไฮไลต์สำหรับการคัดลอกและวางนั้นจะไม่ขยายการไฮไลต์ไปถึงและผ่านเครื่องหมายทวิภาค

การใช้ตัวเลขช่วยให้มั่นใจได้ว่าการไฮไลต์ด้วยดับเบิลคลิกจะทำงานได้กับโปรแกรมใดๆ ที่รองรับสตริง bech32m โดยทั่วไป (ซึ่งรวมถึงตัวเลขอื่นๆ ด้วย) เลข "1" ถูกเลือกเพราะสตริง bech32 ไม่ได้ใช้เลข 1 ในกรณีอื่น เพื่อป้องกันการแปลงโดยไม่ตั้งใจระหว่างเลข "1" กับตัวอักษรพิมพ์เล็ก "l"

และส่วนอื่นของ bech32m address เรียกว่า "ส่วนข้อมูล" (data part) ซึ่งประกอบด้วยสามองค์ประกอบ:

Witness version: ไบต์ถัดไปหลังจากตัวคั่นตัวอักษรนี้แทนเวอร์ชันของ segwit ตัวอักษร "q" คือการเข้ารหัสของ "0" สำหรับ segwit v0 ซึ่งเป็นเวอร์ชันแรกของ segwit ที่มีการแนะนำที่อยู่ bech32 ตัวอักษร "p" คือการเข้ารหัสของ "1" สำหรับ segwit v1 (หรือเรียกว่า taproot) ซึ่งเริ่มมีการใช้งาน bech32m มีเวอร์ชันที่เป็นไปได้ทั้งหมด 17 เวอร์ชันของ segwit และสำหรับ Bitcoin จำเป็นต้องให้ไบต์แรกของส่วนข้อมูล bech32m ถอดรหัสเป็นตัวเลข 0 ถึง 16 (รวมทั้งสองค่า)
Witness program: คือตำแหน่งหลังจาก witnessversion ตั้งแต่ตำแหน่ง 2 ถึง 40 Byte สำหรับ segwit v0 นี้ต้องมีความยาว 20 หรือ 32 Byte ไม่สามารถ
ffมีขนาดอื่นได้ สำหรับ segwit v1 ความยาวเดียวที่ถูกกำหนดไว้ ณ เวลาที่เขียนนี้คือ 32 ไบต์ แต่อาจมีการกำหนดความยาวอื่น ๆ ได้ในภายหลัง
Checksum: มีความยาว 6 ตัวอักษร โดยส่วนนี้ถูกสร้างขึ้นโดยใช้รหัส BCH ซึ่งเป็นประเภทของรหัสแก้ไขข้อผิดพลาด (error corection code) (แต่อย่างไรก็ตาม สำหรับ address บิตคอยน์ เราจะเห็นในภายหลังว่าเป็นสิ่งสำคัญที่จะใช้ checksum เพื่อการตรวจจับข้อผิดพลาดเท่านั้น—ไม่ใช่การแก้ไข

ในส่วนต่อไปหลังจากนี้เราจะลองสร้าง address แบบ bech32 และ bech32m สำหรับตัวอย่างทั้งหมดต่อไปนี้ เราจะใช้โค้ดอ้างอิง bech32m สำหรับ Python

เราจะเริ่มด้วยการสร้างสคริปต์เอาต์พุตสี่ตัว หนึ่งตัวสำหรับแต่ละเอาต์พุต segwit ที่แตกต่างกันที่ใช้ในช่วงเวลาของการเผยแพร่ บวกกับอีกหนึ่งตัวสำหรับเวอร์ชัน segwit ในอนาคตที่ยังไม่มีความหมายที่กำหนดไว้ สคริปต์เหล่านี้แสดงอยู่ในตารางข้างล่างนี้

สำหรับเอาต์พุต P2WPKH witness program มีการผูก commitment ที่สร้างขึ้นในลักษณะเดียวกันกับ P2PKH ที่เห็นใน Legacy Addresses for P2PKH โดย public key ถูกส่งเข้าไปในฟังก์ชันแฮช SHA256 ไดเจสต์ขนาด 32 ไบต์ที่ได้จะถูกส่งเข้าไปในฟังก์ชันแฮช RIPEMD-160 ไดเจสต์ของฟังก์ชันนั้น จะถูกวางไว้ใน witness program

สำหรับเอาต์พุตแบบ pay to witness script hash (P2WSH) เราไม่ได้ใช้อัลกอริทึม P2SH แต่เราจะนำสคริปต์ ส่งเข้าไปในฟังก์ชันแฮช SHA256 และใช้ไดเจสต์ขนาด 32 ไบต์ของฟังก์ชันนั้นใน witness program สำหรับ P2SH ไดเจสต์ SHA256 จะถูกแฮชอีกครั้งด้วย RIPEMD-160 ซึ่งแน่นอนว่าอาจจะไม่ปลอดภัย ในบางกรณี สำหรับรายละเอียด ดูที่ P2SH Collision Attacks ผลลัพธ์ของการใช้ SHA256 โดยไม่มี RIPEMD-160 คือ การผูกพันแบบ P2WSH มีขนาด 32 ไบต์ (256 บิต) แทนที่จะเป็น 20 ไบต์ (160 บิต)

สำหรับเอาต์พุตแบบ pay-to-taproot (P2TR) witness program คือจุดบนเส้นโค้ง secp256k1 มันอาจเป็น public key แบบธรรมดา แต่ในกรณีส่วนใหญ่มันควรเป็น public key ที่ผูกพันกับข้อมูลเพิ่มเติมบางอย่าง เราจะเรียนรู้เพิ่มเติมเกี่ยวกับการผูกพันนั้นในหัวข้อของ taproot

สำหรับตัวอย่างของเวอร์ชัน segwit ในอนาคต เราเพียงแค่ใช้หมายเลขเวอร์ชัน segwit ที่สูงที่สุดที่เป็นไปได้ (16) และ witness program ที่มีขนาดเล็กที่สุดที่อนุญาต (2 ไบต์) โดยมีค่าเป็นศูนย์ (null value)

เมื่อเรารู้หมายเลขเวอร์ชันและ witness program แล้ว เราสามารถแปลงแต่ละอย่างให้เป็น bech32 address ได้ โดยการใช้ไลบรารีอ้างอิง bech32m สำหรับ Python เพื่อสร้าง address เหล่านั้นอย่างรวดเร็ว และจากนั้นมาดูอย่างละเอียดว่าเกิดอะไรขึ้น:

$ github=" https://raw.githubusercontent.com"
        $ wget $github/sipa/bech32/master/ref/python/segwit_addr.py
        $ python
        >>> from segwit_addr import *
        >>> from binascii import unhexlify
        >>> help(encode)
        encode(hrp, witver, witprog)
            Encode a segwit address.
        >>> encode('bc', 0, unhexlify('2b626ed108ad00a944bb2922a309844611d25468'))
        'bc1q9d3xa5gg45q2j39m9y32xzvygcgay4rgc6aaee'
        >>> encode('bc', 0,
        unhexlify('648a32e50b6fb7c5233b228f60a6a2ca4158400268844c4bc295ed5e8c3d626f'))
        'bc1qvj9r9egtd7mu2gemy28kpf4zefq4ssqzdzzycj7zjhk4arpavfhsct5a3p'
        >>> encode('bc', 1,
        unhexlify('2ceefa5fa770ff24f87c5475d76eab519eda6176b11dbe1618fcf755bfac5311'))
        'bc1p9nh05ha8wrljf7ru236awm4t2x0d5ctkkywmu9sclnm4t0av2vgs4k3au7'
        >>> encode('bc', 16, unhexlify('0000'))
        'bc1sqqqqkfw08p'

หากเราเปิดไฟล์ segwit_addr.py และดูว่าโค้ดกำลังทำอะไร สิ่งแรกที่เราจะสังเกตเห็นคือความแตกต่างเพียงอย่างเดียวระหว่าง bech32 (ที่ใช้สำหรับ segwit v0) และ bech32m (ที่ใช้สำหรับเวอร์ชัน segwit รุ่นหลัง) คือค่าคงที่:

BECH32_CONSTANT = 1
        BECH32M_CONSTANT = 0x2bc830a3

และในส่วนต่อไป เราจะเห็นโค้ดที่สร้าง checksum ในขั้นตอนสุดท้ายของการสร้าง checksum ค่าคงที่ที่เหมาะสมถูกรวมเข้ากับข้อมูลอื่น ๆ โดยใช้การดำเนินการ xor ค่าเดียวนั้นคือความแตกต่างเพียงอย่างเดียวระหว่าง bech32 และ bech32m

เมื่อสร้าง checksum แล้ว อักขระ 5 บิตแต่ละตัวในส่วนข้อมูล (รวมถึง witness version, witness program และ checksum) จะถูกแปลงเป็นตัวอักษรและตัวเลข

สำหรับการถอดรหัสกลับเป็นสคริปต์เอาต์พุต เราทำงานย้อนกลับ ลองใช้ไลบรารีอ้างอิงเพื่อถอดรหัส address สอง address ของเรา:

>>> help(decode)
        decode(hrp, addr)
            Decode a segwit address.
        >>> _ = decode("bc", "bc1q9d3xa5gg45q2j39m9y32xzvygcgay4rgc6aaee")
        >>>  _[0], bytes(_[1]).hex()
        (0, '2b626ed108ad00a944bb2922a309844611d25468')
        >>> _ = decode("bc",
                "bc1p9nh05ha8wrljf7ru236awm4t2x0d5ctkkywmu9sclnm4t0av2vgs4k3au7")
        >>> _[0], bytes(_[1]).hex()
        (1, '2ceefa5fa770ff24f87c5475d76eab519eda6176b11dbe1618fcf755bfac5311')

เราได้รับทั้ง witness version และ witness program กลับมา สิ่งเหล่านี้สามารถแทรกลงในเทมเพลตสำหรับสคริปต์เอาต์พุตของเรา:

<version> <program>

ตัวอย่างเช่น:

OP_0 2b626ed108ad00a944bb2922a309844611d25468
        OP_1 2ceefa5fa770ff24f87c5475d76eab519eda6176b11dbe1618fcf755bfac5311

คำเตือน: ข้อผิดพลาดที่อาจเกิดขึ้นที่ควรระวังคือ witness version ที่มีค่า 0 ใช้สำหรับ OP_0 ซึ่งใช้ไบต์ 0x00—แต่เวอร์ชัน witness ที่มีค่า 1 ใช้ OP_1 ซึ่งเป็นไบต์ 0x51 เวอร์ชัน witness 2 ถึง 16 ใช้ไบต์ 0x52 ถึง 0x60 ตามลำดับ

เมื่อทำการเขียนโค้ดเพื่อเข้ารหัสหรือถอดรหัส bech32m เราขอแนะนำอย่างยิ่งให้คุณใช้เวกเตอร์ทดสอบ (test vectors) ที่มีให้ใน BIP350 เราขอให้คุณตรวจสอบให้แน่ใจว่าโค้ดของคุณผ่านเวกเตอร์ทดสอบที่เกี่ยวข้องกับการจ่ายเงินให้กับเวอร์ชัน segwit ในอนาคตที่ยังไม่ได้รับการกำหนด สิ่งนี้จะช่วยให้ซอฟต์แวร์ของคุณสามารถใช้งานได้อีกหลายปีข้างหน้า แม้ว่าคุณอาจจะไม่สามารถเพิ่มการรองรับคุณสมบัติใหม่ ๆ ของบิตคอยน์ได้ทันทีที่คุณสมบัตินั้น ๆ เริ่มใช้งานได้

Private Key Formats

private key สามารถถูกแสดงได้ในหลาย ๆ รูปแบบที่ต่างกันซึ่งสามารถแปลงเป็นตัวเลขขนาด 256 bit ชุดเดียวกันได้ ดังที่เราจะแสดงให้ดูในตารางข้างล่างนี้ รูปแบบที่แตกต่างกันถูกใช้ในสถานการณ์ที่ต่างกัน รูปแบบเลขฐานสิบหก (Hexadecimal) และรูปแบบไบนารี (raw binary) ถูกใช้ภายในซอฟต์แวร์และแทบจะไม่แสดงให้ผู้ใช้เห็น WIF ถูกใช้สำหรับการนำเข้า/ส่งออกกุญแจระหว่างกระเป๋าเงินและมักใช้ในการแสดงกุญแจส่วนตัวแบบ QR code

รูปแบบของ private key ในปัจจุบัน

ซอฟต์แวร์กระเป๋าเงินบิตคอยน์ในยุคแรกได้สร้าง private key อิสระอย่างน้อยหนึ่งดอกเมื่อกระเป๋าเงินของผู้ใช้ใหม่ถูกเริ่มต้น เมื่อชุดกุญแจเริ่มต้นถูกใช้ทั้งหมดแล้ว กระเป๋าเงินอาจสร้าง private key เพิ่มเติม private key แต่ละดอกสามารถส่งออกหรือนำเข้าได้ ทุกครั้งที่มีการสร้างหรือนำเข้า private key ใหม่ จะต้องมีการสร้างการสำรองข้อมูลกระเป๋าเงินใหม่ด้วย

กระเป๋าเงินบิตคอยน์ในยุคหลังเริ่มใช้กระเป๋าเงินแบบกำหนดได้ (deterministic wallets) ซึ่ง private key ทั้งหมดถูกสร้างจาก seed เพียงค่าเดียว กระเป๋าเงินเหล่านี้จำเป็นต้องสำรองข้อมูลเพียงครั้งเดียวเท่านั้นสำหรับการใช้งานบนเชนทั่วไป แต่อย่างไรก็ตาม หากผู้ใช้ส่งออก private key เพียงดอกเดียวจากกระเป๋าเงินเหล่านี้ และผู้โจมตีได้รับกุญแจนั้นรวมถึงข้อมูลที่ไม่ใช่ข้อมูลส่วนตัวบางอย่างเกี่ยวกับกระเป๋าเงิน พวกเขาอาจสามารถสร้างกุญแจส่วนตัวใด ๆ ในกระเป๋าเงินได้—ทำให้ผู้โจมตีสามารถขโมยเงินทั้งหมดในกระเป๋าเงินได้ นอกจากนี้ ยังไม่สามารถนำเข้ากุญแจสู่กระเป๋าเงินแบบกำหนดได้ นี่หมายความว่าแทบไม่มีกระเป๋าเงินสมัยใหม่ที่รองรับความสามารถในการส่งออกหรือนำเข้ากุญแจเฉพาะดอก ข้อมูลในส่วนนี้มีความสำคัญหลัก ๆ สำหรับผู้ที่ต้องการความเข้ากันได้กับกระเป๋าเงินบิตคอยน์ในยุคแรก ๆ

รูปแบบของ private key (รูปแบบการเข้ารหัส)

private key เดียวกันในแต่ละ format

รูปแบบการแสดงผลทั้งหมดเหล่านี้เป็นวิธีต่างๆ ในการแสดงเลขจำนวนเดียวกัน private key เดียวกัน พวกมันดูแตกต่างกัน แต่รูปแบบใดรูปแบบหนึ่งสามารถแปลงไปเป็นรูปแบบอื่นได้อย่างง่ายดาย

Compressed Private Keys

คำว่า compressed private key ที่ใช้กันทั่วไปนั้นเป็นคำที่เรียกผิด เพราะเมื่อ private key ถูกส่งออกไปในรูปแบบ WIF-compressed มันจะมีความยาวมากกว่า private key แบบ uncompressed 1 Byte (เลข 01 ในช่อง Hex-compressed ในตารางด้านล่างนี้) ซึ่งบ่งบอกว่า private key ตัวนี้ มาจากกระเป๋าเงินรุ่นใหม่และควรใช้เพื่อสร้าง compressed public key เท่านั้น

private key เองไม่ได้ถูกบีบอัดและไม่สามารถบีบอัดได้ คำว่า compressed private key จริงๆ แล้วหมายถึง " private key ซึ่งควรใช้สร้าง compressed public key เท่านั้น" ในขณะที่ uncompressed private key จริงๆ แล้วหมายถึง “private key ซึ่งควรใช้สร้าง uncompressed public key เท่านั้น” คุณควรใช้เพื่ออ้างถึงรูปแบบการส่งออกเป็น "WIF-compressed" หรือ "WIF" เท่านั้น และไม่ควรอ้างถึง private key ว่า "บีบอัด" เพื่อหลีกเลี่ยงความสับสนต่อไป

ตารางนี้แสดงกุญแจเดียวกันที่ถูกเข้ารหัสในรูปแบบ WIF และ WIF-compressed

ตัวอย่าง: กุญแจเดียวกัน แต่รูปแบบต่างกัน

สังเกตว่ารูปแบบ Hex-compressed มีไบต์เพิ่มเติมหนึ่งไบต์ที่ท้าย (01 ในเลขฐานสิบหก) ในขณะที่คำนำหน้าเวอร์ชันการเข้ารหัสแบบ base58 เป็นค่าเดียวกัน (0x80) สำหรับทั้งรูปแบบ WIF และ WIF-compressed การเพิ่มหนึ่งไบต์ที่ท้ายของตัวเลขทำให้อักขระตัวแรกของการเข้ารหัสแบบ base58 เปลี่ยนจาก 5 เป็น K หรือ L

คุณสามารถคิดถึงสิ่งนี้เหมือนกับความแตกต่างของการเข้ารหัสเลขฐานสิบระหว่างตัวเลข 100 และตัวเลข 99 ในขณะที่ 100 มีความยาวมากกว่า 99 หนึ่งหลัก มันยังมีคำนำหน้าเป็น 1 แทนที่จะเป็นคำนำหน้า 9 เมื่อความยาวเปลี่ยนไป มันส่งผลต่อคำนำหน้า ในระบบ base58 คำนำหน้า 5 เปลี่ยนเป็น K หรือ L เมื่อความยาวของตัวเลขเพิ่มขึ้นหนึ่งไบต์

TIPจากหลาม: ผมว่าเขาเขียนย่อหน้านี้ไม่ค่อยรู้เรื่อง แต่ความหมายมันจะประมาณว่า เหมือนถ้าเราต้องการเขียนเลข 100 ในฐาน 10 เราต้องใช้สามตำแหน่ง 100 แต่ถ้าใช้ฐาน 16 เราจะใช้แค่ 2 ตำแหน่งคือ 64 ซึ่งมีค่าเท่ากัน

ถ้ากระเป๋าเงินบิตคอยน์สามารถใช้ compressed public key ได้ มันจะใช้ในทุกธุรกรรม private key ในกระเป๋าเงินจะถูกใช้เพื่อสร้างจุด public key บนเส้นโค้ง ซึ่งจะถูกบีบอัด compressed public key จะถูกใช้เพื่อสร้าง address และ address เหล่านี้จะถูกใช้ในธุรกรรม เมื่อส่งออก private key จากกระเป๋าเงินใหม่ที่ใช้ compressed public key WIF จะถูกปรับเปลี่ยน โดยเพิ่มต่อท้ายขนาด 1 ไบต์ 01 ให้กับ private key ที่ถูกเข้ารหัสแบบ base58check ที่ได้จะเรียกว่า "WIF-compressed" และจะขึ้นต้นด้วยอักษร K หรือ L แทนที่จะขึ้นต้นด้วย "5" เหมือนกับกรณีของคีย์ที่เข้ารหัสแบบ WIF (ไม่บีบอัด) จากกระเป๋าเงินรุ่นเก่า

Advanced Keys and Addresses

ในส่วนต่อไปนี้ เราจะดูรูปแบบของคีย์และ address เช่น vanity addresses และ paper wallets

vanity addresses

vanity addresses หรือ addresses แบบกำหนดเอง คือ address ที่มีข้อความที่มนุษย์อ่านได้และสามารถใช้งานได้จริง ตัวอย่างเช่น 1LoveBPzzD72PUXLzCkYAtGFYmK5vYNR33 อย่างที่เห็นว่ามันเป็น address ที่ถูกต้องซึ่งมีตัวอักษรเป็นคำว่า Love เป็นตัวอักษร base58 สี่ตัวแรก addresses แบบกำหนดเองต้องอาศัยการสร้างและทดสอบ private key หลายพันล้านตัวจนกว่าจะพบ address ที่มีรูปแบบตามที่ต้องการ แม้ว่าจะมีการปรับปรุงบางอย่างในอัลกอริทึมการสร้าง addresses แบบกำหนดเอง แต่กระบวนการนี้ต้องใช้การสุ่มเลือก private key มาสร้าง public key และนำไปสร้าง address และตรวจสอบว่าตรงกับรูปแบบที่ต้องการหรือไม่ โดยทำซ้ำหลายพันล้านครั้งจนกว่าจะพบที่ตรงกัน

เมื่อพบ address ที่ตรงกับรูปแบบที่ต้องการแล้ว private key ที่ใช้สร้าง address นั้นสามารถใช้โดยเจ้าของเพื่อใช้จ่ายบิตคอยน์ได้เหมือนกับ address อื่น ๆ ทุกประการ address ที่กำหนดเองไม่ได้มีความปลอดภัยน้อยกว่าหรือมากกว่าที่ address ๆ พวกมันขึ้นอยู่กับการเข้ารหัสเส้นโค้งรูปวงรี (ECC) และอัลกอริทึมแฮชที่ปลอดภัย (SHA) เหมือนกับ address อื่น ๆ คุณไม่สามารถค้นหา private key ของ address ที่ขึ้นต้นด้วยรูปแบบที่กำหนดเองได้ง่ายกว่า address อื่น ๆ

ตัวอย่างเช่น ยูจีเนียเป็นผู้อำนวยการการกุศลเพื่อเด็กที่ทำงานในฟิลิปปินส์ สมมติว่ายูจีเนียกำลังจัดการระดมทุนและต้องการใช้ address ที่กำหนดเองเพื่อประชาสัมพันธ์การระดมทุน ยูจีเนียจะสร้าง address ที่กำหนดเองที่ขึ้นต้นด้วย "1Kids" เพื่อส่งเสริมการระดมทุนเพื่อการกุศลสำหรับเด็ก มาดูกันว่า address ที่กำหนดเองนี้จะถูกสร้างขึ้นอย่างไรและมีความหมายอย่างไรต่อความปลอดภัยของการกุศลของยูจีเนีย

การสร้าง address ที่กำหนดเอง

ควรเข้าใจว่า address ของบิตคอยน์เป็นเพียงตัวเลขที่แสดงด้วยสัญลักษณ์ในรูปแบบตัวอักษร base58 เท่านั้น เพราะฉะนั้นแล้ว การค้นหารูปแบบเช่น "1Kids" สามารถมองได้ว่าเป็นการค้นหาที่อยู่ในช่วงตั้งแต่ 1Kids11111111111111111111111111111 ถึง 1Kidszzzzzzzzzzzzzzzzzzzzzzzzzzzzz มีประมาณ 5829 (ประมาณ 1.4 × 1051) address ในช่วงนั้น ทั้งหมดขึ้นต้นด้วย "1Kids" ตารางด้านล่างนี้แสดงช่วงของ address ที่มีคำนำหน้า 1Kids
ลองดูรูปแบบ "1Kids" ในรูปของตัวเลขและดูว่าเราอาจพบรูปแบบนี้ใน bitcoin address บ่อยแค่ไหน โดยตารางข้างล่างนี้แสดงให้เห็นถีงคอมพิวเตอร์เดสก์ท็อปทั่วไปที่ไม่มีฮาร์ดแวร์พิเศษสามารถค้นหาคีย์ได้ประมาณ 100,000 คีย์ต่อวินาที

ความถี่ของ address ที่กำหนดเอง (1KidsCharity) และเวลาค้นหาเฉลี่ยบนคอมพิวเตอร์เดสก์ท็อป

ดังที่เห็นได้ ยูจีเนียคงไม่สามารถสร้าง address แบบกำหนดเอง "1KidsCharity" ได้ในเร็ว ๆ นี้ แม้ว่าเธอจะมีคอมพิวเตอร์หลายพันเครื่องก็ตาม ทุกตัวอักษรที่เพิ่มขึ้นจะเพิ่มความยากขึ้น 58 เท่า รูปแบบที่มีมากกว่า 7 ตัวอักษรมักจะถูกค้นพบโดยฮาร์ดแวร์พิเศษ เช่น คอมพิวเตอร์เดสก์ท็อปที่สร้างขึ้นเป็นพิเศษที่มีหน่วยประมวลผลกราฟิก (GPUs) หลายตัว การค้นหา address แบบกำหนดเองบนระบบ GPU เร็วกว่าบน CPU ทั่วไปหลายเท่า

อีกวิธีหนึ่งในการหา address แบบกำหนดเองคือการจ้างงานไปยังกลุ่มคนขุด vanity addresses กลุ่มคนขุดvanity addresses เป็นบริการที่ให้ผู้ที่มีฮาร์ดแวร์ที่เร็วได้รับบิตคอยน์จากการค้นหา vanity addresses ให้กับผู้อื่น ยูจีเนียสามารถจ่ายค่าธรรมเนียมเพื่อจ้างงานการค้นหา vanity addresses ที่มีรูปแบบ 7 ตัวอักษรและได้ผลลัพธ์ในเวลาเพียงไม่กี่ชั่วโมงแทนที่จะต้องใช้ CPU ค้นหาเป็นเดือน ๆ

การสร้างที่ address แบบกำหนดเองเป็นการใช้วิธีการแบบ brute-force (ลองทุกความเป็นไปได้): ลองใช้คีย์สุ่ม ตรวจสอบ address ที่ได้ว่าตรงกับรูปแบบที่ต้องการหรือไม่ และทำซ้ำจนกว่าจะสำเร็จ

ความปลอดภัยและความเป็นส่วนตัวของ address แบบกำหนดเอง

address แบบกำหนดเองเคยเป็นที่นิยมในช่วงแรก ๆ ของบิตคอยน์ แต่แทบจะหายไปจากการใช้งานทั้งหมดในปี 2023 มีสาเหตุที่น่าจะเป็นไปได้สองประการสำหรับแนวโน้มนี้:

Deterministic wallets: ดังที่เราเห็นในพาร์ทของการกู้คืน การที่จะสำรองคีย์ทุกตัวในกระเป๋าเงินสมัยใหม่ส่วนใหญ่นั้น ทำเพียงแค่จดคำหรือตัวอักษรไม่กี่ตัว ซึ่งนี่เป็นผลจากการสร้างคีย์ทุกตัวในกระเป๋าเงินจากคำหรือตัวอักษรเหล่านั้นโดยใช้อัลกอริทึมแบบกำหนดได้ จึงไม่สามารถใช้ address แบบกำหนดเองกับ Deterministic wallets ได้ เว้นแต่ผู้ใช้จะสำรองข้อมูลเพิ่มเติมสำหรับ address แบบกำหนดเองทุก address ที่พวกเขาสร้าง ในทางปฏิบัติแล้วกระเป๋าเงินส่วนใหญ่ที่ใช้การสร้างคีย์แบบกำหนดได้ โดยไม่อนุญาตให้นำเข้าคีย์ส่วนตัวหรือการปรับแต่งคีย์จากโปรแกรมสร้าง address ที่กำหนดเอง
การหลีกเลี่ยงการใช้ address ซ้ำซ้อน: การใช้ address แบบกำหนดเองเพื่อรับการชำระเงินหลายครั้งไปยัง address เดียวกันจะสร้างความเชื่อมโยงระหว่างการชำระเงินทั้งหมดเหล่านั้น นี่อาจเป็นที่ยอมรับได้สำหรับยูจีเนียหากองค์กรไม่แสวงหาผลกำไรของเธอจำเป็นต้องรายงานรายได้และค่าใช้จ่ายต่อหน่วยงานภาษีอยู่แล้ว แต่อย่างไรก็ตาม มันยังลดความเป็นส่วนตัวของคนที่จ่ายเงินให้ยูจีเนียหรือรับเงินจากเธอด้วย ตัวอย่างเช่น อลิซอาจต้องการบริจาคโดยไม่เปิดเผยตัวตน และบ็อบอาจไม่ต้องการให้ลูกค้ารายอื่นของเขารู้ว่าเขาให้ราคาส่วนลดแก่ยูจีเนีย

เราไม่คาดว่าจะเห็น address แบบกำหนดเองมากนักในอนาคต เว้นแต่ปัญหาที่กล่าวมาก่อนหน้านี้จะได้รับการแก้ไข

Paper Wallets

paper wallet หรือก็คือ private key ที่พิมพ์ลงในกระดาษ และโดยทั่วไปแล้วมักจะมีข้อมูลของ public key หรือ address บนกระดาษนั้นด้วยแม้ว่าจริง ๆ แล้วมันจะสามารถคำนวณได้ด้วย private key ก็ตาม

คำเตือน: paper wallet เป็นเทคโนโลยีที่ล้าสมัยแล้วและอันตรายสำหรับผู้ใช้ส่วนใหญ่ เพราะเป็นเรื่องยากที่จะสร้างมันอย่างปลอดภัย โดยเฉพาะอย่างยิ่งความเป็นไปได้ที่โค้ดที่ใช้สร้างอาจถูกแทรกแซงด้วยผู้ไม่ประสงค์ดี และอาจจะทำให้ผู้ใช้โดนขโมยบิตคอยน์ทั้งหมดไปได้ paper wallet ถูกแสดงที่นี่เพื่อวัตถุประสงค์ในการให้ข้อมูลเท่านั้นและไม่ควรใช้สำหรับเก็บบิตคอยน์

paper wallet ได้ถูกออกแบบมาเพื่อเป็นของขวัญและมีธีมตามฤดูกาล เช่น คริสต์มาสและปีใหม่ ส่วนเหตุผลอื่น ๆ ถูกออกแบบเพื่อการเก็บรักษาในตู้นิรภัยของธนาคารหรือตู้เซฟโดยมี private key ถูกซ่อนไว้ในบางวิธี ไม่ว่าจะด้วยสติกเกอร์แบบขูดที่ทึบแสงหรือพับและปิดผนึกด้วยแผ่นฟอยล์กันการงัดแงะ ส่วนการออกแบบอื่น ๆ มีสำเนาเพิ่มเติมของคีย์และ address ในรูปแบบของตอนฉีกที่แยกออกได้คล้ายกับตั๋ว ช่วยให้คุณสามารถเก็บสำเนาหลายชุดเพื่อป้องกันจากไฟไหม้ น้ำท่วม หรือภัยพิบัติทางธรรมชาติอื่น ๆ

จากการออกแบบเดิมของบิตคอยน์ที่เน้น public key ไปจนถึง address และสคริปต์สมัยใหม่อย่าง bech32m และ pay to taproot—และแม้แต่การอัพเกรดบิตคอยน์ในอนาคต—คุณได้เรียนรู้วิธีที่โปรโตคอลบิตคอยน์อนุญาตให้ผู้จ่ายเงินระบุกระเป๋าเงินที่ควรได้รับการชำระเงินของพวกเขา แต่เมื่อเป็นกระเป๋าเงินของคุณเองที่รับการชำระเงิน คุณจะต้องการความมั่นใจว่าคุณจะยังคงเข้าถึงเงินนั้นได้แม้ว่าจะเกิดอะไรขึ้นกับข้อมูลกระเป๋าเงินของคุณ ในบทต่อไป เราจะดูว่ากระเป๋าเงินบิตคอยน์ถูกออกแบบอย่างไรเพื่อปกป้องเงินทุนจากภัยคุกคามหลากหลายรูปแบบ

This post and comments are published on Nostr.